Pifagor teoremasini isbotlashning turli usullari: qo'llash, tavsiflash va tushuntirish. Pifagor teoremasini qanday tuzatish mumkin Pifagor

Pifagor teoremasi- Evklid geometriyasining asosiy teoremalaridan biri bo'lib, u maxsus o'rnatadi

to'rtburchaklar trikoning yon tomonlari o'rtasida.

Yunon matematigi Pifagor uni o'z sharafiga olib kelgani muhim, u uning nomi bilan atalgan.

Pifagor teoremasining geometrik formulasi.

Qaytib, Bule teoremasi tajovuzkor darajada tuzilgan:

To'g'ri kesilgan triko uchun kvadratning maydoni, gipotenuzada pobudovanogo, kvadratlar maydonining ko'proq yig'indisi,

kateterlarda uyg'onish.

Pifagor teoremasining algebraik formulasi.

To'g'ri kesilgan trikoda gipotenuzaning uzunligi kvadrati oyoq uzunligi kvadratlarining yig'indisidan kattaroqdir.

Tobto, trikutnik orqali gipotenziya uzunligini bilish c, va dozhini katetiv orqali aі b:

Xafa bo'lgan formulalar Pifagor teoremalari ekvivalent, lekin boshqasiga, formula ko'proq elementar, u emas

Men hududni tushunishim kerak. Boshqa qat'iylik bu soha haqida hech narsa bilmasdan, buzilishi mumkin

vimiryavshi faqat dozhini storin pryamokutny trikutnik.

Pifagorning qaytish teoremasi.

Agar trikotajning bir tomonining kvadrati boshqa ikki tomonning kvadratlari yig'indisiga teng bo'lsa, u holda

trikutnik to'g'ri chiziqli.

Abo, boshqacha qilib aytganda:

Musbat sonlarning uch barobari uchun a, bі c, shu kabi

ísnuê rectocut tricutnik íz oyoqlari aі b bu gipotenuza c.

Teng femoral triko uchun Pifagor teoremasi.

Teng tomonli triko uchun Pifagor teoremasi.

Pifagor teoremasini isbotlang.

Hozirgi vaqtda ilmiy adabiyotlarda teoremaning 367 ta isboti qayd etilgan. Ymovirno, teorema

Ko'p sonli dalillarga ega bo'lgan bitta teoremaga ega Pifagorlar. Raznomanittya oling

faqat geometriya uchun teoremaning asosiy ma'nolari bilan izohlanishi mumkin.

Tushunish, kontseptual jihatdan ularni oz sonli sinflarga bo'lish mumkin. Ulardan ba'zilarini toping:

isbotlash hudud usuli, aksiomatikі ekzotik dalil(masalan,

yordam uchun differensial nisbatlar).

1. Pifagor teoremasini nayranglar orqali isbotlash.

Algebraik formulaning kelajagi isboti bo'ladigan dalillarning eng oddiyidir

aksiomalar bilan vositachisiz. Zokrema figuraning maydonini tushunishda g'olib bo'lmaydi.

Qo'ysangchi; qani endi ABCê to'g'ridan-to'g'ri kesilgan trikotaj C. Keling, balandlikni chizamiz C va ahamiyatli

vv zasnuvannya orqali H.

Trikutnik ACH trikutnikga o'xshaydi AB Uchta kutami. xuddi shunday triko CBH o'xshash ABC.

Kiritilgan belgilar:

qabul qilamiz:

,

Siz nima deb o'ylaysiz -

sklavshi a 2 bu b 2, biz qabul qilamiz:

aks holda, nima olib kelish kerak edi.

2. Pifagor teoremasini yo'l maydoni bilan tasdiqlash.

Qanchalik oddiy bo'lmasin, pastroq ekanligini isbotlang, lekin bu juda oddiy emas. Hammasi hidlanadi

maydonning kuchini yutib oling, Pifagor teoremasining o'zini isbotlash uchun bir necha katlamani isbotlang.

• Ekvivalentlik orqali isbotlash.

Roztashuemo chotiri teng tekis

trikutnik shunday, kichkintoyda ko'rsatilganidek

o'ng qo'l

Yon tomonlari bilan Chotirikutnik c- kvadrat,

ikki gostrih kutyv 90 ° oskylki yig'indisi, va

yondirilgan kesish - 180 °.

Barcha raqamlarning maydoni bir tomondan sog'lom,

uning tomoni bilan kvadrat maydoni ( a+b) va boshqa tomondan, chotiriox trikutnikov i maydoni yig'indisi.

Buni olib kelish uchun nima kerak edi.

3. Pifagor teoremasini cheksiz kichik usul bilan isbotlash.

​

Kresloga qarash, kichkintoyni ko'rsatish va

tomonlarning o'zgarishini himoya qilisha, Biz qila olamiz

keyingi sanani cheksiz muddatga yozib qo'ying

malich yon o'sishhі a(g'alaba shunga o'xshash

trikutnikov):

Vikoristovuyuchi usuli podylu zminnyh, biz bilamiz:

Kattaroq virusli virus har ikkala kateterning turli bosqichlarida gipotenziyani o'zgartiradi:

Ma'lumotlarni, g'alaba qozongan ongni birlashtirib, biz:

Ushbu tartibda biz Bazhan vídpovídíga kelamiz:

Qanchalik muhim emas, qoldiq formulaning kvadratik xatosi chiziqli

yig'indi mustaqil bilan bog'langan bo'lsa ham, trikoning tomonlari va o'sishlar orasidagi mutanosiblik

zbylshennya ryznih catetív shaklida hissalari.

Eng oddiy dalilni olib tashlash mumkin, chunki katetlardan biri kattaroq hisoblanmaydi

(bu vipadka oyog'ida b). Doimiy integratsiya uchun ham xuddi shunday olinadi:

Van der Waerdenning fikriga ko'ra, spívvídnoshennia tuhmat tarzida Bobil uyida miloddan avvalgi 18-asrga yaqin bo'lganligi yanada diqqatga sazovordir. e.

Miloddan avvalgi taxminan 400 roku. Ya'ni, Proklning so'zlariga ko'ra, Platon Pifagor uchliklarini tanib olish uchun algebra va geometriyaga asoslangan usulni bergan. Yulduzgacha 300 ga yaqin. Ya'ni, Evklidning "Kobs"larida Pifagor teoremasining eng qadimgi aksiomatik isboti paydo bo'ldi.

Formula

algebraik dií qasos olish uchun asosiy formula - har qanday teng to'g'ri kesilgan triko, dozhini kateti uchun. a (\displaystyle a)і b (\displaystyle b), va gipotenziya uzunligi - c (\displaystyle c), Vikonano spívvídnoshennia:

.

Raqamlar maydonini tushunishga olib keladigan mumkin bo'lgan va ekvivalent geometrik formulalar: to'rtburchaklar trikoda, kvadratning maydoni, gipotenuzada pobudovannaya, maydonning ko'proq yig'indisi. kvadratchalar, oyoqlarda pobudovanih. Bu nuqtai nazardan, teorema Evklidning quloqlarida tuzilgan.

Pifagorning aylanish teoremasi- har qanday trikotajning to'g'riligi, har qanday pov'yazanning yon tomonining hayoti haqida bayonot a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)). Oxirgi kabi, ijobiy raqamlarning uch barobari uchun a (\displaystyle a), b (\displaystyle b)і c (\displaystyle c), shu kabi a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2))ísnuê oyoqlari bilan tekis kesilgan trikaut a (\displaystyle a)і b (\displaystyle b) bu gipotenuza c (\displaystyle c).

isbotlash

Ilmiy adabiyotda Pifagor teoremasining 400 dan kam isboti qayd etilgan, ular geometriya uchun asosiy qiymatlar kabi natijada elementardir. Asosiy to'g'ridan-to'g'ri dalillar: algebra spívvídnoshen elementlar-trikutnik varianti (masalan, o'xshashlikning mashhur usuli), maydon usuli, shuningdek, turli xil ekzotik dalillar (masalan, differensial rivnían yordami uchun).

Shunga o'xshash fokuslar orqali

Evklidning klassik isboti to'rtburchaklar orasidagi maydonning tekisligini o'rnatish orqali to'g'rilandi, oyoqlari ustida kvadratchalar bo'lgan to'g'ridan-to'g'ri kutdan gipotenuz balandligi ustidan kvadrat bo'shliq bilan o'rnatiladi.

Dizayn, isbot uchun g'olib sifatida: tekis kesilgan trikotaj uchun C (\displaystyle C), oyoqlari ustida kvadrat va gipotenuz ustida kvadrat A B I K (\displaystyle ABIK) balandligi bo'ladi C H (\displaystyle CH) va promin, nima davom etadi, s (\displaystyle s), bu gipotenuzaning ustidagi kvadratni ikkita to'rtburchak i ga ajratadi. To'rtburchaklar maydonining tekisligini o'rnatish bo'yicha yo'nalishni isbotlash A H J K (\displaystyle AHJK) oyoq ustidagi kvadrat bilan A C (\displaystyle AC); gipotenuzaning ustidagi kvadrat hosil qiluvchi boshqa to'rtburchakning maydoni tengligi, boshqa oyoq ustidagi to'rtburchaklar xuddi shunday darajaga o'rnatiladi.

To'rtburchakning Rivnist maydoni A H J K (\displaystyle AHJK)і A C E D (\displaystyle ACED) trikotajlarning uyg'unligi orqali tiklanadi △ A C K ​​(\displaystyle \uchburchak ACK)і △ A B D (\displaystyle \triangle ABD) kvadratchalar maydonining yarmi bilan teri maydoni. A H J K (\displaystyle AHJK)і A C E D (\displaystyle ACED) aftidan, oldinga siljish kuchi bilan bog'lanishda: trikoning maydoni to'rtburchaklar kvadratining yarmini tashkil qiladi, shuning uchun rasm ikki tomon, trikoning yuqori tomoniga balandligi esa boshqa tomonidir. to'rtburchak. Trikotaj buyumlarning bir-biriga mos kelishi ikki tomonning (kvadratchalarning tomonlari) tekisligidan va ular orasidagi kesikdan (to'g'ri kesilgandan buklangan va kesilgan) aniq ko'rinadi. A (\displaystyle A).

Bunday darajada, to'rtburchaklardan tashkil topgan gipotenuza ustidagi kvadratning maydoni isbotlangan. A H J K (\displaystyle AHJK)і B H J I (\displaystyle BHJI), oyoq ustidagi kvadratlar yig'indisi qancha.

Leonardo da Vinchining isboti

Kvadrat usulidan oldin, Leonardo da Vinchi bilimining isboti ham mavjud. Unga to'g'ridan-to'g'ri kesilgan trikoutnik berilsin △ A B C (\displaystyle \uchburchak ABC) tekis kesish bilan C (\displaystyle C) o'sha kvadrat A C E D (\displaystyle ACED), B C F G (\displaystyle BCFG)і A B H J (\displaystyle ABHJ)(Div. chaqaloqlar). Kim tomonda dalil bor H J (\displaystyle HJ) qolgan eski bik trikutnik, mos keladigan bo'ladi △ A B C (\displaystyle \uchburchak ABC), bundan oldin u gipotenusga o'xshardi va qanchalik baland edi (tobto J I = B C (\displaystyle JI = B C)і H I = A C (\displaystyle HI=AC)). Streyt C I (\displaystyle CI) kvadratni buzadi, ikkita teng qismdagi gipotenuzada ko'rsatmalar, trikutnik parchalari △ A B C (\displaystyle \uchburchak ABC)і △ J H I (\displaystyle \uchburchak JHI) uyg'otmoq. Dalil chotirikutniklarning mos kelishini o'rnatadi C A J I (\displaystyle CAJI)і D A B G (\displaystyle DABG), terining z yak maydoni, bir tomondan, oyoqlardagi kvadratlar maydonining yarmidan ko'pi va lateral triko maydoni, boshqa tomondan - yarmidan ko'p ko'rinadi. gipotenuzadagi kvadrat maydoni va tashqi trikotaj maydoni. Shuningdek, oyoq ustidagi kvadrat maydonlarining yarmi yig'indisi gipotenuza ustidagi kvadrat maydonining yarmiga teng, bu Pifagor teoremasining geometrik formulasi bilan bir xil.

Cheksiz kichik usul bilan isbotlash

Menda differensial tenglamalar texnikasiga kiruvchi dalil bor. Zokrema, Hardy g'olibning kateterlarning cheksiz darajada ko'payishiga dalil deb hisoblanadi. a (\displaystyle a)і b (\displaystyle b) va gipotenziya c (\displaystyle c) va tashqi to'g'ri chiziq bilan o'xshashlikka e'tibor bering, shunda u kelayotgan differentsial tezliklarni oldini oladi:

d a d c = c a (displey uslubi (frac (da) (dc)) = (frac (c) (a))), d b d c = c b (displey uslubi (frac (db) (dc)) = (frac (c) (b))).

Ularning kichik o'lchovlari usuli bilan differentsial tenglashtirish chiqariladi c d c = a d a + b d b (displey uslubi c dc = a, da + b, db), integratsiya c 2 = a 2 + b 2 + C o ns t (\displaystyle c^(2)=a^(2)+b^(2)+\mathrm (Const) ). Zastosuvannya kob aqllari a = b = c = 0 (\displaystyle a=b=c=0) 0 ga o'xshash doimiyni tayinlaymiz, bu teoremaning tasdiqlanishiga olib keladi.

Qoldiq formulasidagi kvadratik yotqiziqlar trikotajning yon tomonlari va o'sishlar orasidagi chiziqli mutanosiblik chiziqlari, garchi bu miqdor boshqa toifalarning o'sishidan mustaqil hissalar tufayli bo'lsa ham.

Variantlar va zagalnennya

Uch tomonda o'xshash geometrik raqamlar

Pifagor teoremasining muhim geometrik takomillashtirilishi Evklid tomonidan "Kobslar" asarida berilgan bo'lib, u yon tomonlardagi kvadratlarning kvadratlaridan ko'proq o'xshash geometrik figuralarning maydonlariga o'tadi: bunday raqamlarning maydonlari yig'indisi, oyoqlarda, o'xshash raqamlarning ko'proq joylari, yon tomonlarda.

Butun g'oyaning asosiy g'oyasi geometrik figuraga o'xshash maydon o'zining chiziqli o'lchamining kvadratiga va kvadratning o'z tomonining kvadratiga proportsional ekanligiga asoslanadi. Otzhe, Maydanlardan shunga o'xshash raqamlar uchun A (\displaystyle A), B (\displaystyle B)і C (\displaystyle C), oyoqlarda pobudovanih íz dozhina a (\displaystyle a)і b (\displaystyle b) va gipotenuza c (\displaystyle c) vodpovidno, spivvidnoshnya bo'lishi mumkin:

A a 2 = B b 2 = C c 2 ⇒ A + B = a 2 c 2 C + b 2 c 2 C (displey uslubi (frac (A)(a^(2))))=(frac (B )( b^(2))))=(\frac (C)(c^(2)))\,\O‘ng strelka \,A+B=(\frac (a^(2))(c^(2) )) C+(\frac (b^(2))(c^(2)C).

Pifagor teoremasi orqasida Bo a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)), keyin vikonano.

Bundan tashqari, Pifagor teoremasini qisqartirmasdan keltirish mumkin, ya'ni to'rtburchaklar trikutnikning yon tomonlarida uchta o'xshash geometrik figuralarning maydonlari uchun. A + B = C (\display uslubi A+B=C), keyin Evklid isbotini tasdiqlashning teskari yo'nalishidan Pifagor teoremasining isbotini isbotlash mumkin. Misol uchun, xuddi gipotenuzada to'g'ridan-to'g'ri kesilgan trikotajni kvadrat bilan induktsiya qiling. C (\displaystyle C), va oyoqlarda - kvadratchalar bilan unga o'xshash ikkita tekis kesilgan trikotaj A (\displaystyle A)і B (\displaystyle B), keyin oyoqlardagi trikotlar kob trikutnikining balandligi bilan bo'linishi natijasida o'rnashgan ko'rinadi, ya'ni uchinchisining kattaroq maydonidagi trikutniklarning ikkita kichik maydoni yig'indisi, shunday qilib. daraja A + B = C (\display uslubi A+B=C) va, bunday raqamlar uchun zastosovuyuchi spívvídnoshennia, Pifagor teoremasi kiritiladi.

Kosinus teoremasi

Pifagor teoremasi kosinuslarning umumiy teoremasidan kattaroqning mukammal namunasidir, chunki u yaxshi hiyla-nayrangning tomonlariga to'g'ri keladi:

a 2 + b 2 - 2 a b cos ⁡ th = c 2,

partiyalar orasida de - kut a (\displaystyle a)і b (\displaystyle b). Yakshcho kut dorivnyuê 90 °, keyin cos ⁡ th = 0 (\displaystyle \cos \theta =0) va formula yakuniy Pifagor teoremasiga tushiriladi.

Dovylny trikoutnik

Shuni ta'kidlash kerakki, Pifagor teoremasi faqat spívvídshennym dovzhin storín bo'yicha ishlaydigan ko'proq tricutnikga asoslangan, u birinchi marta Sabiysk astronomi Sobit Ibn Kurroy tomonidan o'rnatilganligi muhimdir. Yangisida yon tomonlari bo'lgan uzun triko uchun yangisiga, yon tomonida asosi bo'lgan teng sonli triko c (\displaystyle c), yon tomonlar bo'ylab yotadigan tashqi tricutnikning tepasidan o'tadigan tepa c (\displaystyle c) va kutami asoslash bilan, teng kutu th (\displaystyle \teta), protil boci c (\displaystyle c). Natijada, oxirgisiga o'xshash ikkita triko o'rnatiladi: birinchisi - uch tomondan a (\displaystyle a), Yozilgan teng-femoral trikoning yonidan uzoqda, bu r (\displaystyle r)- tomonning bir qismi c (\displaystyle c); ikkinchisi yangi tomonga simmetrikdir b (\displaystyle b) yon tomonda s (\displaystyle s)- ikki tomonlama c (\displaystyle c). Natijada, vikonan spívvídnosheniya mavjud:

a 2 + b 2 = c (r + s) (\displaystyle a (2) + b (2) = c (r + s)),

qachon Pifagor teoremasiga aylanadi th = p / 2 (\displaystyle \theta =\pi /2). Spivvídnoshnja ê naslybnosti utavnyh trikutnikov:

c a = a r , c b = b s ⇒ c r + c s = a 2 + b 2 (displey uslubi (frac (c)(a))=(frac (a)(r)),\,(\frac (c) (b) )=(\frac (b)(s))\,\O‘ng strelka \,cr+cs=a^(2)+b^(2)).

Pappus maydoni teoremasi

Evklid bo'lmagan geometriya

Pifagor teoremasi Evklid geometriyasining o'qlariga asoslanadi va Evklid bo'lmagan geometriya uchun haqiqiy emas - Pifagor teoremasi Evklid parallelizmi postulatiga ko'proq tengdir.

Evklid bo'lmagan geometriyada, to'rtburchaklar trikotajning tomonlari orasidagi hizalanish, Pifagor teoremasi bilan kelishilganligi sababli, shaklda obov'yazkovo bo'ladi. Misol uchun, sferik geometriyada to'rtburchaklar trikoning uchta tomoni, xuddi bitta sharning oktanti bilan o'ralgandek, p / 2 (\displaystyle \pi /2), Pifagor teoremasining xurofoti nima

Shu sababli, Pifagor teoremasi giperbolik va elliptik geometriyada o'rinlidir, shuning uchun trikoning to'g'riligini aql bilan bitta bilan almashtira olaman, chunki trikoning ikkita kutiv yig'indisi uchinchisiga qo'shilishi kerak.

Sferik geometriya

Radiusli sharda har qanday to'rtburchak triko uchun R (\displaystyle R)(masalan, yakscho kut at trikutnik to'g'ri) 3 tomoni bilan a, b, c (\displaystyle a, b, c) Tomonlar o'rtasidagi spívvídnoshennia ko'rinishi mumkin:

cos ⁡ (c R) = cos ⁡ (a R) ⋅ cos ⁡ (b R) (\displaystyle \cos \left((\frac(c)(R))\o'ng)=\cos \left((\frac) ) (a)(R))\o'ng)\cdot \cos \left((\frac (b)(R))\o'ng)).

Bu tenglikni sferik kosinus teoremasining o'ziga xos xususiyati sifatida ko'rsatish mumkin, chunki u barcha sferik trikotlar uchun amal qiladi:

cos ⁡ (c R) = cos ⁡ (a R) ⋅ cos ⁡ (b R) + sin ⁡ (a R) ⋅ sin ⁡ (b R) ⋅ cos ⁡ g (\displaystyle \cos \left((\frac () c)(R))\right)=\cos \left((\frac (a)(R))\right)\cdot \cos \left((\frac (b)(R))\right)+\ sin \left((\frac (a)(R))\right)\cdot \sin \left((\frac(b)(R))\o'ng)\cdot \cos \gamma). ch ⁡ c = ch ⁡ a ⋅ ch ⁡ b (\displaystyle \operator nomi(ch) c=\operator nomi (ch),

de ch (\displaystyle \operator nomi (ch) )- Giperbolik kosinus. Tsya formula ê keling, uni giperbolik kosinus teoremasining bir turi deb ataymiz, chunki u barcha fokuslar uchun amal qiladi:

ch ⁡ c = ch ⁡ a ⋅ ch ⁡ b - sh ⁡ a ⋅ sh ⁡ b ⋅ cos ⁡ g (\displaystyle \operatorname(ch) c=\operatorname (ch) a\cdot \operatorname (ch) (sh) a \cdot \operatorname (sh) b\cdot \cos \gamma ),

de g (\displaystyle\gamma)- Qut, uning tepasi qarama-qarshi tomonda c (\displaystyle c).

Giperbolik kosinus uchun Teylor seriyasi ( ch ⁡ x ≈ 1 + x 2/2 (\displaystyle \operator nomi (ch) x\taxminan 1+x^(2)/2)) giperbolik trikoutnik qanday o'zgarishini ko'rsatishingiz mumkin (agar a (\displaystyle a), b (\displaystyle b)і c (\displaystyle c) nolga), keyin to'g'ri kesilgan trikutnikning giperbolik kengaytmalari klassik Pifagor teoremasining kengaytmalariga yaqinlashadi.

Zastosuvannya

dvuhyryh pryamokutnyh tizimlarida Vídstanov

Pifagor teoremasining eng muhim qo'llanilishi to'rtburchaklar, tizim, koordinatalardagi ikki nuqta orasidagi farqni aniqlashdir: s (\displaystyle s) koordinatali nuqtalar o'rtasida (a,b) (\displaystyle (a,b))і (c, d) (\displaystyle (c, d)) biri:

s = (a - c) 2 + (b - d) 2 (\displaystyle s=(\sqrt ((a-c)^(2)+(b-d)^(2)))).

Kompleks sonlar uchun Pifagor teoremasi kompleks son modulining qiymati uchun tabiiy formulani beradi - uchun z = x + y i (\displaystyle z = x + yi) vino

Teorema

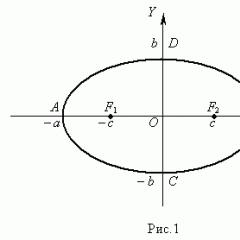
To'g'ri kesilgan trikoda gipotenuzaning uzunligi kvadrati oyoq uzunligi kvadratlarining yig'indisidan kattaroqdir (1-rasm):

$c^(2)=a^(2)+b^(2)$

Pifagor teoremasining isboti

Trikaut $A B C$ toʻgʻri galstukli $C$ boʻlsin (2-rasm).

Yuqoridan $ C $ dan gipotenuza $ A B $ gacha balandlik chizamiz, balandlikning asosi ma'noli $ H $ dir.

To'rtburchak $A C H$ trikuti ikki burmali $A B C$ trikutiga o'xshaydi ($\angle A C B=\angle C H A=90^(\circ)$, $\angle A$ - yumaloq). Xuddi shunday, $C B H$ $A B C$ ga o'xshaydi.

Vivshi belgisi

$$B C=a, A C=b, A B=c$$

s shunga o'xshash trikutnikov otrimuemo, scho

$$\frac(a)(c)=\frac(H B)(a), \frac(b)(c)=\frac(A H)(b)$$

Zvidsi maêmo, scho

$$a^(2)=c \cdot H B, b^(2)=c \cdot A H$$

G'ayratni siqib chiqaring, olib qo'ying

$$a^(2)+b^(2)=c \cdot H B+c \cdot A H$$

$$a^(2)+b^(2)=c \cdot(H B+A H)$$

$$a^(2)+b^(2)=c \cdot A B$$

$$a^(2)+b^(2)=c \cdot c$$

$$a^(2)+b^(2)=c^(2)$$

Buni olib kelish uchun nima kerak edi.

Pifagor teoremasining geometrik formulasi

Teorema

Gipotenuzada induktsiya qilingan kvadrat maydonining to'g'ridan-to'g'ri kesilgan trikotaji uchun oyoqlarda induktsiya qilingan kvadrat maydonlarining ko'proq yig'indisi (2-rasm):

Vazifalar yechimini qo'llang

dumba

Menejer. Topshiriq to'g'ri chiziqli triko $A B C$, oyoqlari uzunligi 6 sm va 8 sm.Bu trikoning gipotenuzasini toping.

Yechim. Zgídno z umovoy oyoq $a=6$ sm, $b=8$ sm.

$c^(2)=a^(2)+b^(2)=6^(2)+8^(2)=36+64=100$

Gipotenuzaning ahmoq ekanligini hisobga olish kerak

$c = \sqrt(100) = 10$(sm)

Vidpovid. 10 sm

dumba

Menejer. To'g'ri kesilgan trikoning maydonini toping, chunki oyog'ining biri ikkinchisidan 5 sm kattaroq, gipotenuzasi esa 25 sm uzunroq ekanligi aniq.

Yechim.$x$ sm - kichikroq oyoqning uzunligi, keyin $(x+5)$ sm - kattasining uzunligi bo'lsin. Pifagor teoremasi bilan bir xil narsa bo'lishi mumkin:

$$x^(2)+(x+5)^(2)=25^(2)$$

Arklarni ochish, shunga o'xshashlarni yasash va virishuemo otrimane kvadratini tekislash:

$x^(2)+5 x-300=0$

Vídpovídno teoremagacha Víêt, otrimuêmo, scho

$x_(1)=15$ (sm) , $x_(2)=-20$ (sm)

$x_(2)$ qiymati aql ongini qoniqtirmaydi, shuning uchun kichikroq oyog'i 15 divs, kattasi esa 20 divs.

To'g'ri kesilgan triko matoning kvadrati ko'proq dojin yoga katetiviga o'xshaydi, tobto

$$S=\frac(15 \cdot 20)(2)=15 \cdot 10=150\left(\mathrm(sm)^(2)\o'ng)$$

Vidpovid.$S=150\chap(\mathrm(sm)^(2)\o'ng)$

Tarixiy dalil

Pifagor teoremasi- Evklid geometriyasining asosiy teoremalaridan biri, bu to'rtburchaklar trikotajning tomonlari o'rtasida parallellikni o'rnatadi.

Qadimgi xitoycha "Chjou bi suan jing" kitobida tomonlari 3, 4 va 5 bo'lgan Pfagor trikoti haqida bor. Eng buyuk nemis matematika tarixchisi Moritz Kantor (1829 - 1920) $3^(2)+4^( paritet ekanligini biladi. 2)=5^ (2) $ misrliklarga miloddan avvalgi 2300-yillardayoq ma'lum bo'lgan. Men o'ylaganimdek, budilniklar 3, 4 va 5 tomonlari bo'lgan to'g'ridan-to'g'ri kesilgan trikolarning yordami uchun hali ham to'g'ri edi. Bobilliklar orasida Pifagor teoremasi haqida ko'proq ma'lumot. Bitta matnda to'g'ridan-to'g'ri kesilgan rivnofemoral trikutnikning gipotenuzasini hisoblash yaqinlashtiriladi.

Hozirgi vaqtda ilmiy adabiyotlarda teoremaning 367 ta isboti qayd etilgan. Imovirno, Pifagor teoremasi juda ko'p dalillarga ega bo'lgan yagona teoremadir. Bunday farqni faqat geometriya uchun teoremaning asosiy ma'nolari bilan izohlash mumkin.

Ijodkorlik salohiyati gumanitar fanlarga, tabiiy ravishda tahlilga, amaliy g'oyalarga va formulalar va raqamlarning quruq tiliga boy bo'lishi kerak. Matematika gumanitar fanlarga tegishli emas. "Barcha fanlar malikasi" dagi ijodsiz ale uzoqqa bormaydi - odamlar bu haqda uzoq vaqtdan beri bilishadi. Masalan, Pifagorning uch soati.

Shkílni podruchniki, afsuski, matematikada nafaqat teoremalar, aksiomalar va formulalarni siqish muhimligini tushuntirish uchun chaqirmang. Asosiy tamoyillarni tushunish va tushunish muhimdir. Va siz o'z fikringizni markalar va abet haqiqatlaridan o'rganishga harakat qilganingizda - faqat shunday onglarda barcha buyuk g'oyalar odamlardir.

Bunday xulosalarga bugungi kunda Pifagor teoremasini biladiganlarni qo'shish mumkin. Ushbu yordam bilan biz matematikaning nafaqat qodirligini, balki men ahmoq bo'lishim mumkinligini ko'rsatishga harakat qilamiz. Va bu kostyum nafaqat bunday ko'zoynaklardagi botaniklarga, balki kuchli aql va kuchli ruhga ega bo'lgan har bir kishiga mos keladi.

Oziqlanish tarixidan

Garchi bu teorema "Pifagor teoremasi" deb atalsa ham, Pifagorning o'zi buni isbotlamagan. To'g'ri kesilgan trikoutnik va maxsus kuchlar yangisiga qaytdi. Oziq-ovqat zanjiriga qarang. Bitta versiya uchun Pifagor teoremaning to'liq isbotini birinchi bo'lib bilgan. Boshqa har qanday dalil uchun Pifagorning muallifligini aytib bo'lmaydi.

Bugun siz kimning yurishi va kimning rahm-shafqati haqida o'ylamaysiz. Vídomo kamroq, scho Pifagorni isbotladi, yakscho g'alaba qozondi, agar uxlab qolsa, u saqlanmadi. Vtym, Evklidning "Pochatkív" dan mashhur dalil Pifagorga tegishli bo'lishi mumkin, deb uzr bor, va Evklid yogo faqat sobit.

Bugungi kunda, shuningdek, to'g'ridan-to'g'ri trikotaj haqidagi ko'rsatmalar fir'avn Amenemhet I ning Misr soatlarida, shoh Hammurabi davrida Bobil loy lavhalarida, qadimgi hindlarning "Sulva Sutra" risolasida va qadimgi " Yakshanba Xitoy ijodi”.

Baxit singari, Pifagor teoremasi so'nggi soatlarda matematiklarning ongini band qildi. Tasdiqlash uchun bugungi kunda tasdiqlangan 367 ga yaqin turli xil dalillar mavjud. Kim uchun u boshqa teorema bilan raqobatlasha olmaydi. Mashhur dalillar mualliflari orasida Leonardo da Vinchi va AQShning yigirmanchi prezidenti Jeyms Garfildni taxmin qilish mumkin. Hammasi matematika uchun teoremaning birlamchi ahamiyati haqida gapirishga arziydi: uni ko'rsatish kerak, aks holda geometriyaning ko'proq teoremalari u bilan bog'liq.

Pifagor teoremasini isbotlang

Maktab yordamchilari uchun algebraik dalillarni keltirib chiqarish muhimdir. Ammo geometriyadagi teoremaning mohiyati, unda keling, oldingizda bizni ko'rib chiqamiz va shu fanga asoslangan mashhur teoremani isbotlaymiz.

Isbot 1

To'rtburchak triko uchun Pifagor teoremasining eng oddiy isboti uchun ideal fikrni o'rnatish kerak: triko nafaqat to'g'ri chiziqli, balki teng femoral bo'lsin. Eslatib o'taman, bunday ayyorning o'zi qadimgi matematikaga qaragan.

Tasdiqlash "kvadrat, to'rtburchaklar trikoning gipotenuzasiga oid takliflar, kvadratlarning teng yig'indisi, yoga oyoqlaridagi takliflar" yaqinlashib kelayotgan kreslolar bilan tasvirlanishi mumkin:

ABCning tekis sonli tekis kesilgan trikosiga hayron bo'ling: AC gipotenuzasida siz bir nechta trikolardan iborat kvadrat hosil qilishingiz mumkin, bu tashqi ABC uchun yaxshi. Va AB va PS oyoqlarida kvadrat shaklida taklif qilingan, bularning terilari ikkita o'xshash trikotaj bilan almashtirilishi kerak.

Nutqdan oldin suvga cho'mish ko'plab latifalar va karikaturalar, Pifagor teoremasiga asos bo'ldi. Eng mashhur, ehtimol, tse "Har tomondan Pifagor shimlari":

Isbot 2

Bu usul algebra va geometriya bilan birlashtirilgan va matematik Bxaskari tomonidan qadimgi hind isbotining bir varianti sifatida qaralishi mumkin.

3 tomoni bilan to'g'ridan-to'g'ri kesilgan trikutda turing a, b va c(1-rasm). Keling, ikkita katetning dojinlari yig'indisiga teng tomonlari bo'lgan ikkita kvadratni eslaylik, - (a+b). Kvadratchalar terisida, 2 va 3-rasmlardagi kabi uyg'oning.

Birinchi kvadratda kichik 1 kabi nayranglardan chotir yasang. Natijada ikkita kvadrat hosil bo'ladi: biri a tomoni bilan, ikkinchisi tomoni bilan. b.

Boshqa kvadratda chotiri shunga o'xshash trikolarni boshqa tomondan kvadrat yasashga undadi, bu eng qulay gipotenuzdir. c.

2-rasmdagi kvadratlar kvadratlarining yig'indisi biz 3-rasmda z tomoni bilan ishlagan kvadratning maydoniga teng. Anjirdagi kvadratlarning maydonini o'zgartirib, bu haqda o'ylash oson. 2 formula ortida. Kichkintoydagi chizilgan kvadratning maydoni 3. Aytgancha, o'zaro teng bo'lgan chotirioks maydoni to'rtburchaklar trikotaj maydonidan joylashgan. u200b narigi tarafdagi katta maydon (a+b).

Hamma narsani yozib bo'lgach, ehtimol: a 2 + b 2 \u003d (a + b) 2 - 2ab. Qo'llarni oching, kerakli algebraik hisob-kitoblarni bajaring va nimani olib tashlang a 2 + b 2 = a 2 + b 2. Tsiomda 3-rasmda yozilgan maydon. kvadratlarni an'anaviy formuladan foydalanib hisoblash mumkin S=c2. Tobto. a2+b2=c2- Siz Pifagor teoremasini tugatdingiz.

Isbot 3

XII asrda "Vinets znannya" ("Siddhanta shiromani") risoladagi tavsiflarning juda qadimgi hind isboti va asosiy dalil sifatida g'olibning chaqirig'i muallifi matematik iste'dodlarga va olimlar va izdoshlarning hushyorligiga murojaat qiladi: " Voy-buy!".

Ale mi, keling, kattaroq hisobotning isbotini ko'rib chiqaylik:

Kresloda ko'rsatilgandek, kvadratning o'rtasida chotiri to'g'ridan-to'g'ri kesilgan trikutniklar qoling. Katta kvadratning yon tomonida sezilarli darajada gipotenuz mavjud h. Trikutnikning oyoqlari deyiladi Aі b. Vídpovídno ichki kvadratning kreslo tomoniga (a-b).

Kvadratning maydoni formulasini toping S=c2, tashqi kvadratning maydonini hisoblash uchun. I bir soat ichida ichki kvadratning maydonini va barcha to'rtburchak trikotajning maydonini qo'shib bir xil qiymatni o'zgartiring: (a-b) 2 2+4*1\2*a*b.

Kvadrat maydonni hisoblashning turli xil variantlari orasidan tanlashingiz mumkin, shunda ular bir xil natijani berishi uchun qayta ko'rib chiqishingiz mumkin. Men sizga nima yozish huquqini beraman c 2 =(a-b) 2 +4*1\2*a*b. Qaror natijasida siz Pifagor teoremasining formulasini olasiz c2=a2+b2. Teorema tugallandi.

Isbot 4

Ushbu qadimiy xitoycha dalil, "Tanlangan stelet" nomini o'tkazib yuborgan holda - men barcha takliflar natijasida stela figurasiga o'taman:

Yangisi stullarni qo'lga kiritadi, chunki biz allaqachon 3-rasmda boshqa dalilga bo'ysundik. Va takliflar tomoni bilan ichki kvadrat bir xil bo'ladi, eski hind isboti sifatida, ko'proq induktsiya.

1-rasmdagi kresloga moslash uchun g'oya sifatida ikkita to'g'ridan-to'g'ri kesilgan yashil trikotaj, ularni z tomoni va gipotenuslari bilan kvadratning qarama-qarshi tomonlariga o'tkazing, buzkovy trikutniklarning gipotenuslariga qo'llang, so'ngra rasm ostidagi rasm. nomi "steletz nomli" (2-rasm). Aniqlik uchun siz qog'oz kvadratchalar va trikolar bilan xuddi shunday qilishingiz mumkin. Siz "sovg'agan odam" ikkita kvadratdan iborat ekanligiga aralashib qoldingiz: yon tomondagi kichkina kvadratchalar. b men ajoyib zi tomoni a.

Qi pobudovi qadimgi xitoylik matematiklarga ruxsat berdi va biz ularga ergashishimiz kerak edi c2=a2+b2.

Isbot 5

Pifagor teoremasining yechimini bilishning yana bir usuli bu geometriyaga tayanishdir. U "Garfild usuli" deb ataladi.

To'g'ridan-to'g'ri kesilgan trikoutnikda qoling ABC. Biz nima olib kelishimiz kerak ND 2 \u003d AC 2 + AB 2.

Kim uchun oyog'ini davom ettirish kerak AC va hushyor turing CD, bu yaxshiroq oyoq AB. Perpendikulyarlarni tushirish AD vydrizok ED. Vidrizki EDі AC teng. Ulanish nuqtalari Eі Da, shu qatorda; shu bilan birga Eі V va stulni biroz pastroqqa olib tashlang:

Minorani olib kelish uchun biz yana sinab ko'rgan usulga o'tamiz: biz ko'rgan figuraning maydonini ikki jihatdan bilamiz va uni birga solishtiramiz.

Bagatokutnikning kvadratini biling YOTOQ u utvoryuyut kabi uchta trikutnik maydonini buklab, mumkin. Va ulardan biri ECB, nafaqat tik, balki rívnofemoral. Shuni unutmaylik AB = CD, AC = EDі BC = PЄ- Yogoni bosib olmaslik uchun yozishingizni so'rashimizga yo'l qo'ymang. Otzhe, S ABED \u003d 2 * 1/2 (AB * AC) + 1 / 2BC 2.

Kim bilan, bu aniq YOTOQ- Trapesiya. Shuning uchun men formula uchun maydonni hisoblayman: S ABED = (DE + AB) * 1/2AD. Bizning hisobimiz uchun shamollarni ko'rsatish osonroq va yaxshiroq AD pul summasi kabi ACі CD.

Keling, raqamlar maydonini hisoblashning haqoratli usullarini yozamiz, ular orasidagi tenglik belgisini qo'yamiz: AB*AC+1/2BC 2 =(DE+AB)*1/2(AC+CD). Vikoristovuêmo allaqachon bizga ma'lum va vídrízkív ko'proq ekvivalentini tasvirlangan, rekord o'ng qismini kechirish uchun: AB*AC+1/2BC 2 =1/2(AB+AC) 2. Va endi biz kamarlarni ochamiz va muvozanatni o'zgartiramiz: AB*AC+1/2BC 2 =1/2AC 2 +2*1/2(AB*AC)+1/2AB 2. Barcha o'zgarishlarni tugatgandan so'ng, biz kerakli narsalarni olib tashlaymiz: ND 2 \u003d AC 2 + AB 2. Biz teoremani keltirdik.

Albatta, bu dalillar ro'yxati to'liq emas. Pifagor teoremasini vektorlar, kompleks sonlar, differensial tengliklar, stereometriya ham yordamga keltirishi mumkin. Men fizikadan dars beraman: masalan, kvadrat stullar va triko obsyagidagi o'xshash tasvirlarda vatanni to'ldiring. Ona vatanni quyish orqali maydonning tengligini va natijaning teoremasini keltirish mumkin.

Pifagor uchliklari haqida bir necha so'z

Maktab dasturiga qo'shilmaydigan odamlar kam. Va kunning bu vaqtida, cicavia va mayning archasi geometriyada katta ahamiyatga ega. Pifagor uchliklari boy matematik muammolarni bajarish uchun zastosovuyutsya. Ular haqidagi e'lon kelajakda siz uchun yaxshi bo'lishi mumkin.

Xo'sh, Pitagoriyalik uchlik nima? Bu uchta tomonidan tanlangan natural sonlarning nomi, ulardan ikkitasining kvadratlari yig'indisi kvadratdagi uchinchi raqamga teng.

Pifagor uchliklari quyidagilar bo'lishi mumkin:

• ibtidoiy (barcha uchta raqam o'zaro oddiy);
• ibtidoiy emas (uchlikning teri raqami bir xil raqamga ko'paytirilsa, biz yangi uchlikni ko'ramiz, ibtidoiy emas).

Bizning davrimizga qadar qadimgi misrliklarni Pifagor uchliklarining soni manikasi hayratda qoldirdi: ular badbo'y hiddan 3,4 va 5 tomonlari bo'lgan to'g'ridan-to'g'ri kesilgan trikotajni ko'rishlari mumkin edi. Nutqdan oldin, hiyla-nayrang bo'lsin, uning tomonlari Pfagor uchligining raqamlariga teng, chunki qulflar to'g'ri.

Pifagor uchliklarini qo'llang: (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20) ) ), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34) , (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45) , ( 14 48, 50), (30, 40, 50) va boshqalar.

Teoremaning amaliy isboti

Pifagor teoremasi matematikada, arxitekturada va kundalik hayotda, astronomiyada va ilhomlantiruvchi adabiyotda saqlanib qolganligi ma'lum.

Kundalik hayot haqida eslatma: Pifagor teoremasini boshqa darajadagi katlamaning boshlarida yangi keng stantsiyada bilish. Masalan, Romanesk uslubiga hayron bo'ling:

Oynaning kengligi sezilarli darajada b katta pívkolning bir xil radiusi sifatida tan olinishi mumkin R va orqali b: R=b/2. Kichikroq pivkolning radiusi ham orqali ko'rinadi b: r=b/4. Biz viknaning ichki qoziq radiusini aytishimiz kerak (yogo deb ataladi p).

Pifagor teoremasi R. Kim uchun vikorist to'g'ridan-to'g'ri kesilgan trikouterdir, lekin biroz ma'nosi uchun nuqta chiziq. Trikoning gipotenuzasi ikkita radiusdan iborat: b/4+p. Bir oyog'i radius. b/4, insh b/2-p. Vikoristovuyuchi Pifagor teoremasi, biz yozamiz: (b/4+p) 2 =(b/4) 2 +(b/2-p) 2. Dali rozkriyomo ta'zim qiladi va olib ketadi b 2 /16+ bp / 2 + p 2 \u003d b 2 / 16 + b 2 / 4-bp + p 2. Keling, bu virusni yoqaylik bp/2=b 2 /4-bp. Va keyin biz barcha a'zolarni ajratamiz b, biz shunga o'xshash taklif qilamiz, olib tashlaymiz 3/2*p=b/4. Natijada biz buni bilamiz p=b/6- Bizga nima kerak.

Qo'shimcha teorema uchun siz qo'sh dahu uchun er-xotin krokvi hisoblashingiz mumkin. Shunisi e'tiborga loyiqki, mobil telefon ulanishining balandligi signal qo'shiq joyiga etib borishi kerak. Va Moskva Maydanida barqaror ravishda yangi yalinka qurish. Bachit singari, bu teorema nafaqat yordamchilarning yon tomonlarida yashaydi, balki ko'pincha haqiqiy hayotning natijasiga aylanadi.

Adabiyotga kelsak, Pifagor teoremasi yozuvchilarni antik soatlar davomida bo'g'ib qo'ygan va bizning davrimiz uchun ishlashda davom etmoqda. Misol uchun, 19-asr nemis yozuvchisi Adelbert fon Chamisso sonetni yozishda xo'rsindi:

Haqiqat nuri tez orada yonmaydi,
Ale, e'lon qilib, u o'sishi dargumon
Men, xuddi ming yil oldin,
sumnívív i superechki deb qo'ng'iroq qilmang.

Naimudrishi, qarasam
Haqiqat nuri, xudolar gapiradi;
Men yuz urdi, pichoqladim, yotibman.
Pifagorning e'tirofidan sovg'a.

O'sha soatdan boshlab zarblar vahshiyona bo'ldi:
Naviki bichache qabilasini xavotirga soldi
Podiya, taxmin qildim.

Keling, taslim bo'laylik: eksa o'qi, soat keldi,
Men yana qurbonlik qilmoqchiman
Qanday ajoyib teorema.

(Viktor Toporov tomonidan tarjima qilingan)

Va 20-asrda radianlik yozuvchi Evgen Veltistov "Fit Electronics" kitobida Pifagor teoremasini isbotlab, Pifagor teoremasini isbotladi. Va ikki dunyo dunyosi haqida ko'proq va ko'proq rozpovídí, qanday bir lahza, Pifagor teoremasi asosiy qonun bo'ldi va olingan butun dunyo dinini singdirish kabi, amalga oshirish edi. Yangi dunyoda hayot ancha oson, ale va juda zerikarli bo'lar edi: masalan, "yumaloq" va "momiq" so'zlarining ma'nosini tushunish yo'q.

Shuningdek, “Fit Elektronika” kitobida ham muallif matematika o‘qituvchisi Taratarning so‘zlari bilan: “Matematikaning boshi bor – fikr, yangi g‘oyalar” degandek. Aqlning juda ijodiy siyosati Pifagor teoremasini tug'diradi - bu juda ko'p turli xil dalillarga ega ekanligi bejiz emas. Von unli tovushdan tashqariga qarashga yordam beradi va tanish nutqni yangi usulda hayratda qoldiradi.

Visnovok

Ushbu maqola siz maktablararo matematika dasturlarini ko'rib chiqishingiz va "Geometriya 7-9" (L.S.Atanasyan, V.M.Rudenko) va "Geometriya 7" qo'llanmalarida ko'rsatilgan Pifagor teoremasini isbotlash haqida ko'proq ma'lumot olishingiz uchun yaratilgan. -11 ”(A.V. Pogorelov), ale va ínshí tsíkaví yo'llari mashhur teorema olib keladi. Va shuningdek, Pifagor teoremasi g'ayrioddiy hayotda zastosovuvatsya mumkin kabi, uni qo'llash.

Avvalo, ushbu ma'lumot sizga matematika darslarida eng yuqori ball olish uchun ariza topshirish imkonini beradi - qo'shimcha bo'yinlardan olingan fan natijalari har doim yuqori baholanadi.

Boshqacha qilib aytganda, biz sizga matematika qanchalik fan ekanligini ko'rishga yordam bermoqchi edik. Muayyan dumba ustida Perekonatisya, scho zavzhd ê m_sce ijodkorligi. Pifagor teoremasi sizni mustaqil hazillar va matematika va boshqa fanlar bo'yicha yomon sharhlarga ilhomlantiradigan shunday maqola ekanligiga shubha qilamiz.

Izohlarda bizga ayting, maqolada nimani topdingiz, buni isbotlang. Bosh ofisda sizga qi kerak edi. Pifagor teoremasi va ushbu maqola haqida fikringizni bizga yozing - biz siz bilan hamma narsani muhokama qilishdan xursand bo'lamiz.

blog.website, asl nusxada yuborilgan materialning yangi yoki shaxsiy nusxasi bilan.

Pifagor teoremasi: Oyoqlarda spiral bo'lgan kvadrat kvadratlar yig'indisi ( aі b), gipotenuzada chaqirilgan kvadratning qo'shimcha maydoni ( c).

Geometrik formulalar:

Qaytib, Bule teoremasi tajovuzkor darajada tuzilgan:

Algebraik formula:

Tobto, trikutnik orqali gipotenziya uzunligini bilish c, va dozhini katetiv orqali aі b :

a 2 + b 2 = c 2

Teoremaning tajovuzkor formulasi ekvivalentdir, lekin aks holda formula ko'proq elementar bo'lib, bu sohani tushunishni anglatmaydi. Buning uchun yana bir qattiqlikni buzish mumkin, bu hudud haqida hech narsa bilmasdan, faqat to'g'ridan-to'g'ri kesilgan trikutnikning yon tomonlarini o'ldirgan.

Pifagorning qaytish teoremasi:

isbotlash

Hozirgi vaqtda ilmiy adabiyotlarda teoremaning 367 ta isboti qayd etilgan. Imovirno, Pifagor teoremasi juda ko'p dalillarga ega bo'lgan yagona teoremadir. Bunday farqni faqat geometriya uchun teoremaning asosiy ma'nolari bilan izohlash mumkin.

Tushunish, kontseptual jihatdan ularni oz sonli sinflarga bo'lish mumkin. Ulardan: maydon usuli bilan isbotlash, aksiomatik va ekzotik isbotlar (masalan, differensial tenglamalar yordamida).

Shunga o'xshash fokuslar orqali

Algebraik formulaning navbatdagi isboti aksiomalarning orqasida turgan isbotlarning eng oddiyidir. Zokrema, bu raqamning maydonini tushunish g'olib emas.

Qo'ysangchi; qani endi ABCê to'g'ridan-to'g'ri kesilgan trikotaj C. Keling, balandlikni chizamiz Cí mazmunli її asosi orqali H. Trikutnik ACH trikutnikga o'xshaydi ABC ikki bo'limda. xuddi shunday triko CBH o'xshash ABC. Vivshi belgisi

qabul qilinadi

Ekvivalent nima

Qichqir, ol

Maydon usuli bilan isbotlang

Qanchalik oddiy bo'lmasin, pastroq ekanligini isbotlang, lekin bu juda oddiy emas. Barcha hidlar hududning kuchini qozonadi, Pifagor teoremasining o'zini isbotlash uchun qandaydir katlamalarni isbotlaydi.

Ekvivalentlik orqali isbotlash

1. Roztashuemo chotiri to'g'ridan-to'g'ri kesilgan trikutniklar shunday, kichik birida ko'rsatilgandek 1.
2. Yon tomonlari bilan Chotirikutnik cê kvadrat, ikkita gostrikh kutiv yig'indisining parchalari 90 ° va ochiq kut - 180 °.
3. Barcha raqamlarning maydoni qattiq, bir tomondan kvadratning maydoni (a + b), boshqa tomondan trikotaj kvadratlari va ikkita ichki kvadratlarning yig'indisi.

Buni olib kelish uchun nima kerak edi.

Ekvivalentlik orqali isbotlang

Qo'shimcha qayta tartibga solish ortida oqlangan dalil

Ushbu dalillardan birining dumbasi o'ng qo'lli kresloda ko'rsatilgan, de kvadrat, gipotenuzada, ikki kvadratga o'tishda, oyoqlarda so'rash.

Evklidning isboti

Evklidning isboti oldidagi kreslo

Evklidning isbotidan oldingi illyustratsiya

Evklidni isbotlash g'oyasi tajovuzkor: biz gipotenuzada pobudovannaya kvadrat maydonining yarmini, pobudovannyh kvadratlar maydonining yarmi yig'indisidan ko'proq olib chiqishga harakat qilamiz. oyoqlarda, hatto katta va ikkita kichik kvadratning maydoni teng.

Keling, kresloni ko'rib chiqaylik. Yangi mitti to'rtburchaklar uchburchakning yon tomonlarida kvadratchalar yasadik va to'g'ri bo'lakning tepasidan C promin gipotenuzasiga perpendikulyar ravishda AB, ko'tarilgan kvadrat ABIK, gipotenuzaga surilgan ikkita to'rtburchaklar - BHJI va HAKJ aniq. Ko'rinib turibdiki, bu to'rtburchaklar maydonlari o'ng oyoqlarga joylashtirilgan kvadratlarning maydonlariga to'liq teng.

Keling, DECA kvadratining maydoni AHJK to'rtburchaklar maydoniga teng ekanligini aniqlashga harakat qilaylik. Oxirgi narsa - trikotaj maydonini balandlik poydevorining yarmi sifatida belgilash. Birinchi ogohlantirishdan ko'rasizki, ACK trikosining maydoni AHK trikosining maydonidan (kichkintoyda ko'rsatilmagan), yak, uning orqa tomonida, maydonning yarmidan ko'p. tekis kesilgan AHJK.

Aytaylik, ACK trikosining maydoni ham DECA maydonining yarmini tashkil qiladi. Buning uchun zarur bo'lgan yagona narsa ACK va BDA trikotajlarining tengligini ta'minlashdir (BDA trikotaj maydonining parchalari buyurtma qilingan quvvat uchun kvadrat maydonining yarmiga teng). Tenglik yaqqol ko'rinib turibdi, trikolar ikkala tomonda teng, ular orasida kutku. Xuddi shunday - AB=AK,AD=AC - CAK va BAD kesmalarining tekisligini harakat usuli bilan keltirish oson: CAK trikautini strelka qarshisida 90° ga burang, bundan tashqari, ikkita trikautning yon tomonlari ham aniq. qaraladi, kengaytiriladi (kvadrat tepasidagi kut orqali - 90°).

BCFG kvadrati va BHJI to'rtburchaklar maydonining tekisligi haqidagi kuzatuv mutlaqo o'xshash.

Timning o'zi shuni ko'rsatdiki, gipotenuzada induktsiya qilingan kvadrat maydoni oyoqlarda induktsiya qilingan kvadratlar maydonidan hosil bo'ladi. Qaysi dalil g'oyasi qo'shimcha animatsiya uchun qo'shimcha ravishda tasvirlangan, chunki u yanada rivojlangan.

Leonardo da Vinchining isboti

Leonardo da Vinchining isboti

Isbotning asosiy elementi simmetriya va ruhdir.

Kresloga qarang, simmetriyadan ko'rinib turibdiki, vydryzok CI pushti kvadrat ABHJ ikkita bir xil qismda (trikutnik parchalari ABCі JHI pobudova uchun teng). Koristuyuchisya yil strelkasiga qarshi 90 gradusga burilsa, biz chizilgan raqamlarning tengligini vbachayemo qilamiz. CAJI і GDAB . Endi ma'lum bo'ldiki, biz tomonidan soyalangan raqamning maydoni oyoqlarda joylashgan kvadratlar maydonining yarmi yig'indisidan ko'proq, bu maydon \u200b tashqi triko. Boshqa tomondan, gipotenuzaga joylashtirilgan kvadrat maydonining boshqa yarmida, shuningdek, tashqi trikotaj maydoni. Qolgan dalillar o'qilishi kutilmoqda.

Cheksiz kichik usul bilan isbotlash

Differensial tenglamalar yordami uchun haqoratli dalil ko'pincha 20-asrning birinchi yarmida tirik bo'lgan mashhur ingliz matematigi Hardiga tegishli.

Kresloga qarash, kichkintoyni ko'rsatish va tomonning o'zgarishini kuzatish a, biz tomonlarning cheksiz kichik o'sishi uchun spívvídnoshenya boshlanishini yozishimiz mumkin hі a(trikutnikovga o'xshash vikorist):

Cheksiz kichik usul bilan isbotlash

Podylu zminnyh usuli bilan Koristuyuchis, biz bilamiz

Ko'proq gal virusi har ikki oyoqning turli bosqichlarida gipotenziyani o'zgartiradi

Berilgan teng va g'alabali boshoqlarni integratsiyalash, aql, otrimuemo

c 2 = a 2 + b 2+ doimiy.

Bu tartibda, biz Bazhan vídpovídí kelamiz

c 2 = a 2 + b 2 .

Qanchalik katta bo'lmasin, qoldiq formuladagi kvadratik yotqizish trikotaj tomonlari va o'sishlar orasidagi chiziqli mutanosiblik chiziqlaridir, garchi yig'indi boshqa toifalarning o'sishidagi mustaqil yotqizishlarga bog'liq bo'lsa ham.

Eng oddiy dalil, oyoqlardan biri o'smaganligining dalili sifatida qabul qilinishi mumkin (bu holda, oyoqlar b). Keyin doimiy integratsiya uchun olinadi

Variantlar va zagalnennya

• Agar siz boshqa shunga o'xshash raqamlarning oyoqlaridagi kvadratlarni almashtirmoqchi bo'lsangiz, Pifagor teoremasi amalga oshadi: To'g'ridan-to'g'ri kesilgan triko o'xshash figuralarning maydonlari yig'indisiga ega bo'lib, ular oyoqlarda, ko'proq raqamlar maydonlarida gipotenuzada induktsiya qilinadi. Zokrema:
  • Oyoqlarda uyg'ongan muntazam trikotlar maydonining yig'indisi, gipotenuzada uyg'ongan to'g'ri trikutnikning qo'shimcha maydoni.
  • Oyoqlarda pivkolív, pobudovannyh (diametri kabi), dorívnyuê pívkolív, pívkolív, gipotenuzada pobudovanogo maydoni yig'indisi. Bu dumba ikki kilogrammli yoylar bilan o'ralgan va gipokrat oylari nomini kiygan raqamlarning kuchini isbotlashda g'alaba qozonadi.

Tarix

Chu-Pey miloddan avvalgi 500-200 yillar Zliva yozgan: balandlik va poydevor uzunligi kvadratlarining yig'indisi gipotenziya uzunligi kvadratidir.

Qadimgi Xitoy kitobida Chu-Pei, 3, 4 va 5 tomonlari bo'lgan Pifagor trikolari haqida bir hikoya bor: Bu kitobda Bashari hind geometriyasining kreslolaridan biri bilan ishlaydigan kichkintoylar taklifi mavjud.

Kantor (eng yirik nemis matematika tarixchisi) 3 + 4 + 5 = tengligi miloddan avvalgi 2300 yildayoq misrliklarga ma'lum bo'lganini biladi. e .., qirol Amenemhat I soatlari uchun (Berlin muzeyiga papirus 6619 bilan gidno). Kantorning fikriga ko'ra, harpedonapti yoki tortuvchi bobinlar 3, 4 va 5 tomonlari bo'lgan to'g'ridan-to'g'ri kesilgan trikutniklar yordami uchun to'g'ri kuti edi.

Xuddi shunday yo'l tutish ham osonroq. Keling, 12 m uzunlikdagi shamol o'tkazgichni olib, uni erining rangiga qarab 3 m uzunlikda bog'laymiz. bir chorakdan va boshqasidan 4 metr. Zavdovkaning 3 va 4 metrli tomonlari o'rtasida to'g'ridan-to'g'ri kut ulangan ko'rinadi. Harpedonaptlarni rad qilish mumkin edi, ularning yo'li bizni ishg'ol qilishga undaydi, go'yo, masalan, barcha duradgorlar bilan turg'un bo'ladigan yog'och o'roq mashinasi bilan tezlashdi. Misrlik kichkintoylar bor, ularda bunday vosita ishlatiladi, masalan, duradgorning ishini ifodalovchi kichiklar.

Bobilliklar orasida Pifagor teoremasi haqida ko'proq ma'lumotlar mavjud. Hammurapi davriga qadar, ya'ni miloddan avvalgi 2000 yilgacha bo'lgan bir matnda. Ya'ni, to'g'ri kesilgan trikutnikning gipotenuzasini hisoblashga yaqinroq rahbarlik qilish. Zvydsi siz nevtíshny visnovka qilishingiz mumkin, Dvorichchya da ular ba'zi vipadkalarning haddan tashqari yaqinlashishi bilan to'g'ridan-to'g'ri kesilgan trikutniklar bilan ishlashga muvaffaq bo'lishdi. Bir tomondan, Misr va Bobil matematikasining hozirgi bilimlariga, ikkinchi tomondan, yong'oqning tanqidiy gulchambariga asoslanib, van der Vaerden (gollandiyalik matematik) shunday o'rashni amalga oshirdi:

Adabiyot

Rossiya meniki

• Skopets Z.A. Geometrik miniatyuralar. M., 1990 yil
• Yelenskiy Sh. Pifagorga ergash. M., 1961 yil
• Van der Vaerden B. L. Uyg'ongan fan. Qadimgi Misr, Bobil va Gretsiya matematikasi. M., 1959 yil
• Glazer G.I. Maktabda matematika tarixi. M., 1982 yil
• Sankt-Litzman, Pifagor teoremasi, Moskva, 1960 yil.
  • V. Litzmanning kitobidan olingan materialning ko'plab dalillari bilan Pifagor teoremasi haqidagi sayt, ko'plab kreslolar ko'p sonli grafik fayllarda taqdim etilgan.
• Pifagor teoremasi va Pifagor uchliklari, D. V. Anosovning "Matematikaga qarash va uni ko'rish" kitobining 3-bobi.
• Pifagor teoremasi va isbotlash usullari haqida G. Gleyzer, Rossiya Badiiy Akademiyasi akademigi, Moskva.

Ingliz

• WolframMathWorld da Pifagor teoremasi
• Cut-The-Knot, Pifagor teoremasiga bag'ishlangan bo'lim, 70 ga yaqin dalillar va qo'shimcha ma'lumotlar (inglizcha)

Wikimedia fondi. 2010 yil.