Probabilistic and statistical methods are applicable. Statistical methods. Statistical analysis of specific data
When conducting psychological and pedagogical studies, an important role is assigned to mathematical methods for modeling processes and processing experimental data. These methods should include, first of all, the so-called probabilistic-statistical methods of research. This is due to the fact that many random factors have a significant impact on behavior of both a separate person in the process of its activities and a person in the team. Accident does not allow to describe phenomena within the framework of deterministic models, since it is manifested as insufficient regularity in mass phenomena and, therefore, does not allow to predict the onset of certain events with accuracy. However, in the study of such phenomena, certain patterns are detected. An irregularity, characteristic of random events, with a large number of tests, is usually compensated by the appearance of statistical patterns, stabilizing the frequencies of random events. Consequently, these random events have a certain probability. There are two fundamentally different probabilistic statistical methods of psychological and pedagogical research: classic and non-classical. We carry out a comparative analysis of these methods.
Classic probabilistic statistical method. The classical probability statistical research method is based on the theory of probabilities and mathematical statistics. This method is used in the study of massive random phenomena, it includes several stages, the main of which are the following.
1. Building a probabilistic model of reality, based on the analysis of statistical data (determination of the law of the distribution of random variable). Naturally, the patterns of mass random phenomena are expressed all the more distinctly, the greater the volume of statistical material. The sample data obtained during the experiment is always limited and are strictly speaking, random character. In this regard, an important role is given to the generalization of the patterns obtained on the sample, and the distribution of them for the entire general set of objects. In order to solve this problem, a certain hypothesis about the nature of the statistical pattern is adopted, which manifests itself in the studied phenomenon, for example, the hypothesis that the phenomenon underdeveloped is subject to the law of normal distribution. Such a hypothesis is called zero hypothesis, which may be erroneous, therefore, along with zero hypothesis, an alternative or competing hypothesis is still put forward. Checking how far the experimental data obtained correspond to a statistical hypothesis is carried out using the so-called non-parametric statistical criteria or consent criteria. Currently, the criteria for the consent of Kolmogorov, Smirnov, Omega-Square, etc. are widely used. The main idea of \u200b\u200bthese criteria consists in measuring the distance between the function of the empirical distribution and the function of a fully known theoretical distribution. The methodology for testing statistical hypothesis is strictly designed and sets out in a large number of works on mathematical statistics.
2. Conduct the necessary calculations with mathematical means in the framework of the probabilistic model. In accordance with an established probabilistic phenomenon, the characteristic parameters are calculated, for example, such as mathematical expectation or mean, dispersion, standard deviation, mod, median, asymmetry, etc.
3. Interpretation of probabilistic statistical conclusions in relation to the real situation.
Currently, the classic probabilistic statistical method is well developed and is widely used in conducting research in various fields of natural, technical and social sciences. A detailed description of the essence of this method and its use to solve specific tasks can be found in a large number of literary sources, such as in.
Non-classical probabilistic statistical method. The non-classical probably statistical research method differs from the classic in that it is applied not only to mass, but also to individual events that have a fundamentally accidental character. This method can be effectively used in analyzing the behavior of an individual in the process of performing a particular activity, for example, in the process of learning to learn students. Features of the non-classical probabilistic-statistical method of psychological and pedagogical studies Consider on the example of the behavior of students in the process of learning knowledge.
For the first time, a probabilistic-statistical model of the behavior of students in the process of learning knowledge was proposed in work. The further development of this model was done in the work. The doctrine as a type of activity, the purpose of which the acquisition by the person of knowledge, skills and skills depends on the level of development of the consciousness of the student. The structure of consciousness includes such cognitive processes, as a feeling, perception, memory, thinking, imagination. An analysis of these processes shows that they are inherent in the elements of chance due to the random nature of the mental and somatic states of the individual, as well as physiological, psychological and information noise when working on a brain. The latter led to the description of the processes of thinking to failure to use the model of the deterministic dynamic system in favor of the model of a random dynamic system. This means that the determinism of consciousness is implemented through an accident. From here, it can be concluded that the knowledge of a person who is actually a product of consciousness, also have a random character, and, therefore, a probabilistic-statistical method can be used to describe the behavior of each individual student in the process of learning knowledge.
In accordance with this method, the student is identified by the distribution function (probability density), which determines the likelihood of finding it in a unit area of \u200b\u200binformation space. In the process of learning, the distribution function with which the student is identified, evolving, is moving in the information space. Each student has individual properties and is allowed independent localization (spatial and kinematic) individuals relative to each other.
Based on the law of conservation of the likelihood, a system of differential equations representing the continuity equations that bind the change in the probability density per unit of time in the phase space (coordinate space, speeds and accelerations of various orders) with the divergence of the probability density flow in the phase space under consideration. The analysis of the analytical solutions of a number of continuity equations (distribution functions) characterizing the behavior of individual students in the learning process.
When conducting experimental studies of students' behavior in the process of learning, probabilistic statistical scaling is used, according to which the measurement scale is an ordered system.
1. Finding experimental distribution functions According to the results of the control event, for example, the exam. The typical view of the individual distribution functions found when using a twenty-bullure scale is presented in Fig. 1. The method of finding such functions is described in.
2. Display distribution functions to numerical space. For this purpose, the calculation of moments of individual distribution functions. In practice, as a rule, it is enough to limit ourselves to the definition of the moments of the first order (mathematical expectation), the second order (dispersion) and the third order characterizing the asymmetry of the distribution function.
3. Ranking of students in terms of knowledge based on the comparison of the moments of various orders of their individual distribution functions.
Fig. 1. A typical view of the individual functions of the distribution of students who received various assessments on the exam in general physics: 1 - a traditional rating "2"; 2 - traditional rating "3"; 3 - traditional rating "4"; 4 - traditional rating "5"
On the basis of the additivity of individual distribution functions in the experimental distribution functions for students' stream (Fig. 2).

Fig. 2. Evolution of the full function of the distribution of the stream of students, approximated by smooth lines: 1 - after the first year; 2 - after the second year; 3 - after the third year; 4 - after the fourth course; 5 - after the fifth course
Analysis of the data presented in Fig. 2 shows that as progress in the information space, the distribution function is blurred. This is due to the fact that the mathematical expectations of the functions of the distribution of individuals move with different speeds, and the functions themselves are blurred due to the dispersion. A further analysis of these distribution functions can be carried out within the framework of a classic probabilistic statistical method.
The discussion of the results. Analysis of the classical and non-classical probabilistic statistical methods of psychological and pedagogical studies has shown that there is a significant difference between them. It, as this can be understood from the above, is that the classical method is applicable only to analyzing mass events, and the non-classical method is applicable to both the analysis of mass and single events. In this regard, the classical method can be conditionally called a mass probabilistic statistical method (MVSM), and the non-classical method is an individual probabilistic statistical method (IVSM). In 4], it was shown that none of the classical methods for assessing students' knowledge within the framework of a probability-statistical model of an individual cannot be applied to these purposes.
Distinctive features of MVSM and IVSM methods will look at the example of measuring the completeness of students' knowledge. For this purpose, we will conduct a mental experiment. Suppose there is a large number of absolutely identical psychic and physical characteristics of students who have the same prehistory, and let them, without interacting with each other, at the same time participate in the same cognitive process, experiencing an absolutely identical strictly deterministic effect. Then, in accordance with the classical ideas about the objects of measurement, all students would have to obtain the same estimates of the completeness of knowledge with any given measurement accuracy. However, in reality, with a sufficiently large accuracy of measurements of the assessment of the completeness of students' knowledge will be different. It is not possible to explain this measurement result within the framework of the MVSM, since it is initially assumed that the impact on absolutely identical non-consistent students has a strictly deterministic nature. The classic probabilistic statistical method does not take into account that the determinism of the process of knowledge is implemented through an accident, internally inherent in each person around the world.
The random nature of the student behavior in the process of learning knowledge takes into account the IVSM. The use of an individual probability statistical method for analyzing the behavior of the idealized team under consideration would show that it is impossible to indicate exactly the position of each student in the information space, it is only possible to speak the probabilities of finding it in a particular area of \u200b\u200binformation space. In fact, each student is identified by the individual distribution function, with its parameters, such as mathematical expectation, dispersion, etc., individual for each student. This means that the individual distribution functions will be located in different areas of the information space. The reason for such behavior of students is the random nature of the process of knowledge.
However, in some cases, the research results mined within the MVSM can be interpreted in the framework of the IVSM. Suppose that the teacher in assessing the student's knowledge uses a five-point measurement scale. In this case, the error in the assessment of knowledge is ± 0.5 points. Therefore, when the student is an assessment, for example, 4 points, this means that his knowledge is in the interval of 3.5 points to 4.5 points. In fact, the position of the individual in the information space in this case is determined by the rectangular function of the distribution, the width of which is equal to the measurement error of ± 0.5 points, and the assessment is a mathematical expectation. This error is so big that it does not allow to observe the true kind of distribution function. However, despite the coarse approximation of the distribution function, the study of its evolution allows you to obtain important information as the behavior of a separate individual and the group of students in general.
The result of measuring the completeness of the student's knowledge is directly or indirectly affected by the consciousness of the teacher (meter), which is also characteristic of the accident. In the process of pedagogical measurements, there are actually the interaction of two random dynamic systems that identify the behavior of the student and the teacher in this process. The interaction of the student subsystem with the faculty subsystem is considered and it is shown that the speed of the mathematical expectation of the individual functions of the distribution of students in the information space is proportional to the function of the impact of the faculty-teaching team and inversely proportional to the function of inertia, characterizing the disjustness of the change in the position of the mathematical expectation in space (analogue of Aristotel's Law in mechanics).
Currently, despite significant achievements in the development of theoretical and practical frameworks of measurements during psychological and pedagogical research, the problem of measurements in general is still far from solving. This is due primarily to the fact that there is still no sufficient information on the effect of consciousness on the measurement process. A similar situation has developed in solving the problem of measurements in quantum mechanics. Thus, in the work, when considering the conceptual problems of quantum measurement theory, it is stated that resolve some paradoxes of measurements in quantum mechanics "... It is unlikely possible without the immediate inclusion of an observer consciousness into a theoretical description of the quantum measurement." Further it is said that "... consistent is the assumption that consciousness can make a certain event, even if, according to the laws of physics (quantum mechanics), the likelihood of this event is small. We will make an important clarification of the wording: the consciousness of this observer can probably see this event. "
In scientific knowledge, a complex, dynamic, holistic, subordinated system of diverse methods attached at different stages and levels of knowledge is functioning. Thus, in the process of scientific research, various general scientific methods and means of knowledge of both empirical and theoretical levels are applied. In turn, general scientific methods, as already noted, include a system of empirical, overall and theoretical methods and means of cognition of real reality.
1. Outer profile methods of scientific research
Overtiseral methods are used primarily on theoretical level of scientific research, although some of them can be applied on the empirical level. What are these methods and what is their essence?
One of them widely used in a scientific study is analysis method (from Greek. Analysis - decomposition, dismemberment) - the method of scientific knowledge, which is a mental dismemberment of the object under study on the component elements in order to study its structure, individual signs, properties, internal relations, relationships.
The analysis makes it possible to the researcher to penetrate the phenomenon being studied by dismembering it into the components of the elements and identify the main thing significant. Analysis as a logical operation is part of an integral part into any scientific research and usually forms its first stage, when the researcher moves from an unintended description of the object being studied to identify its structure, composition, as well as its properties, connections. The analysis is already present on the sensual stage of knowledge, turns on in the process of sensation and perception. At the theoretical level of knowledge, the highest form of analysis is beginning to function - mental, or an abstract-logical analysis, which arises with the skills of logistically dismemberment of objects in the process of labor. Gradually, a person mastered the ability to predict material and practical analysis in a mental analysis.
It should be emphasized that, being a necessary admission of knowledge, the analysis is only one of the moments of the process of scientific research. It is impossible to know the essence of the subject, only dismembering it on the elements from which it consists. For example, a chemist, according to Hegel, puts a piece of meat into his retort, exposes it to a variety of operations, and then declares: I found that the meat consists of oxygen, carbon, hydrogen, etc. But these substances - elements are no longer the essence of meat .
In each area of \u200b\u200bknowledge, there is as if their limit of the object membership, followed by the nature of the properties and patterns. When the analysis of particular is studied, the next stage of cognition occurs - synthesis.
Synthesis (From Greek. Synthesis - a compound, a combination, compilation) is a method of scientific knowledge, which is a mental compounds of the components, elements, properties, links of the object under study, dissected as a result of the analysis, and the study of this object as a whole.
Synthesis is not an arbitrary, eclectic connection of parts, elements of the whole, and a dialectic integer with the selection of essence. The result of the synthesis is a completely new education, whose properties are not only an external connection of these components, but also the result of their internal relationship and interdependence.
The analysis records mainly the specific, which distinguishes parts from each other. Synthesis reveals that significant common, which binds the parts into a single whole.
The researcher mentally dismeasisizes the subject to composite parts in order to first detect these parts themselves, find out what is a whole, and then consider it as consisting of these parts already examined separately. Analysis and synthesis are in dialectical unity: our thinking is equally analytically, how many synthetic.
Analysis and synthesis take their origin in practical activities. Constantly displaced in its practical activity, various items on their components, a person gradually learned to share objects and mentally. The practical activity was not only from the dismemberment of objects, but also from the reunification of parts into a single whole. On this basis, mental analysis and synthesis gradually arose.
Depending on the nature of the study of the object and the depth of penetration into its essence, various types of analysis and synthesis are applied.
1. Direct or empirical analysis and synthesis - applies, as a rule, at the stage of superficial familiarization with the object. This type of analysis and synthesis makes it possible to know the phenomena of the object being studied.
2. Elementary-theoretical analysis and synthesis - is widely used as a powerful instrument of knowledge of the essence of the studied phenomenon. The result of the use of such analysis and synthesis is to establish causal relationships, identifying various patterns.
3. Structural and genetic analysis and synthesis - allows you to make the most deeply aimed in the essence of the object being studied. This type of analysis and synthesis requires the decay in the complex phenomenon of such elements, which represent the most important, substantial and have a decisive effect on all other parties under the object being studied.
Methods for analyzing and synthesis in the process of scientific research are functioning in an inseparable connection with the abstraction method.
Abstraction (from Lat. Abstractio - distraction) is an overall method of scientific knowledge, which is a mental distraction from insignificant properties, links, relations of studied objects with the simultaneous mental allocation of the essential, aspects of the researchers of the parties, properties, links of these items. Its essence is that the thing, property or relationship mentally stand out and at the same time be distracted from other things, properties, relationships, and is considered as if in "pure form".
Abstraction in human mental activity has a versatile nature, because each step of thought is associated with this process, or using its results. The essence of this method is that it allows you to mentally be distracted from insignificant, secondary properties, links, relations of objects and at the same time mentally allocate, to record the research of the parties, properties, links of these items.
There is a process of abstraction and the result of this process, which is called abstraction. Usually, the result of abstraction is understood as knowledge of some sides of the objects studied. The abstraction process is a set of logical operations leading to such a result (abstraction). Examples of abstractions include countless concepts, which operates a person not only in science, but also in everyday life.
The question of the fact that in objective reality is allocated by the abstractioning work of thinking and from which thinking is distracted, in each particular case, it is solved depending on the nature of the object being studied, as well as the objectives of the study. During its historical development, science dates back from one level of abstractness to another, higher. The development of science in this aspect is, according to V. Heisenberg, "Deploying abstract structures". The decisive step into the scope of abstraction was made when people mastered the score (number), thereby discovering the path leading to mathematics and mathematical science. In this regard, V. Heisenberg notes: "The concepts originally received by abstraction from a specific experience gain their own life. They turn out to be more informative and productive than it could be expected at first. In subsequent development, they detect their own design opportunities: they contribute to the construction of new forms And concepts, allow you to establish links between them and may be applicable in our attempts to understand the world of phenomena in our attempts. "
A brief analysis suggests that abstraction is one of the most fundamental cognitive logical operations. Therefore, it acts as the most important method of scientific research. The abstract method is closely related to the method of generalization.
Generalization - the logical process and the result of a mental transition from one to a common one, from less common to more common.
Scientific generalization is not just a mental allocation and synthesis of similar signs, and the penetration into the essence of the thing: the discretion of one in the diverse, in common, in a single, natural in random, as well as the combination of objects on similar properties or links into homogeneous groups, classes.
In the process of generalization, a transition is made from single concepts to general, from less general concepts - to more general, from single judgments - to the general, from the judgments of a smaller community - to the judgment of greater generality. Examples of such a generalization can be: a mental transition from the concept of "mechanical form of motion of matter" to the concept of "the form of motion of matter" and in general "movement"; from the concept of "spruce" to the concept of "coniferous plant" and in general "plant"; From judgment "This metal electrically conductive" to the judgment "All metals of electrically conductive".
The scientific research is most often used by the following types of generalization: inductive when the researcher comes from individual (isolated) facts, events to their overall expression in thoughts; The logical when the researcher comes from one, less common, thoughts to another, more general. The generalization limit are philosophical categories that cannot be generalized as they do not have a generic concept.
A logical transition from more general thought to a less general is the process of restriction. In other words, this is a logical operation, reverse summary.
It must be emphasized that the ability of a person to abstraction and a generalization has developed and developed on the basis of public practice and mutual communication of people. It is of great importance both in the cognitive activity of people and in the overall progress of the material and spiritual culture of society.
Induction (from lat. I nductio - guidance) - the method of scientific knowledge, in which the general conclusion is knowledge about the whole class of objects obtained as a result of the study of individual elements of this class. In induction, the thought of the researcher comes from private, single through a special and universal one. Induction, as a logicalization of the study, is associated with the generalization of the results of observations and experiments, with the movement of thought from one to common. Since the experience is always endless and not full, the inductive conclusions always have a problematic (probabilistic) character. Inductive generalizations are usually considered as experienced truths or empirical laws. The direct basis of induction is the repeatability of reality phenomena and their signs. Receiving similar features from many subjects of a certain class, we conclude that these features are inherent in all subjects of this class.
By the nature of the output distinguish the following main groups of inductive conclusions:
1. Full induction is such a conclusion in which the general conclusion about the class of items is made on the basis of the study of all items of this class. Full induction gives reliable conclusions, because it is widely used as evidence in a scientific study.
2. Incomplete induction is such a conclusion in which the total output is obtained from the parcels that do not cover all the items of this class. There are two types of incomplete induction: popular, or induction through a simple listing. It is a conclusion in which the general conclusion about the class of objects is made on the grounds that there was not a single contrary to generalization among the observed facts; Scientific, i.e., the conclusion in which the general conclusion about all objects of the class is made on the basis of knowledge of the necessary signs or causing connections in part of the subjects of this class. Scientific induction can give not only probability, but also reliable conclusions. Scientific induction is inherent in their methods of knowledge. The fact is that establishing the causal connection of the phenomena is very difficult. However, in some cases, this relationship can be established using logical techniques, called the methods of establishing causal relations, or methods of scientific induction. There are five such methods:
1. Method of single similarity: if two or more cases of the studied phenomenon have only one circumstance, and everyone, the remaining circumstances are different, then this is the only similar circumstance and is the reason for this phenomenon:
Consequently - + and there is a reason a.
In other words, if the preceding circumstances of ABC cause the phenomena of ABC, and the circumstances are ADE - the appearance of the ADE, then the conclusion is made that A is the reason A (or that the phenomenon A and is causally connected).
2. Method of the only difference: If cases in which the phenomenon occurs or does not occur, differ only in one: - preceding circumstances, and all other circumstances are identical, then this is one circumstance and is the reason for this phenomenon:
In other words, if the preceding circumstances of ABC cause the phenomenon of ABC, and the circumstances of the Sun (phenomenon A is eliminated during the experiment) cause a phenomenon of the aircraft, then the conclusion is made that but is the reason a. The basis of such a conclusion is the disappearance of A during the elimination of A.
3. The combined method of similarities and differences is a combination of the first two methods.
4. Method of related changes: If the occurrence or change of one phenomenon, it is necessary to make a certain change in another phenomenon, then both of these phenomena are in causal communication with each other:
Change and change a
Unchanged in, with
Therefore, there is the reason a.
In other words, if when the previous phenomenon is changed, the observed phenomena A changes, and the remaining preceding phenomena remain unchanged, then it can be concluded that a cause a.
5. The remnant method: if it is known that the cause of the studied phenomenon does not serve the circumstances necessary for it, except for one, then this circumstance is probably the cause of this phenomenon. Using the remnant method, the French astronomer Neptune predicted the existence of the planet Neptune, which he soon and opened German Astronomer Galle.
The considered methods of scientific induction to establish causal connections are most often applied is not isolated, but in relationships, complementing each other. Their value depends mainly on the degree of probability of the conclusion that one or another method gives. It is believed that the most powerful method is the difference method, and the lowest method is similarity. The remaining three methods occupy an intermediate position. This difference in the value of methods is based mainly on the fact that the method of similarity is mainly observed, and the method of differences - with an experiment.
Even a brief description of the induction method allows you to make sure of its dignity and importance. The significance of this method is primarily in close connection with the facts experiment, with practice. In this regard, F. Bacon wrote: "If we mean to penetrate the nature of things, we are everywhere we appeal to induction. For we believe that induction is a real form of evidence that protects feelings from all kinds of delusions, closely followed by nature, bordering And almost merging with practice. "
In modern logic, induction is considered as a theory of probabilistic output. Attempts are made to formalize the inductive method based on the ideas of the theory of probability, which will help more clearly understand the logical problems of this method, as well as determine its heuristic value.
Deduction (from lat. Deductio - excretion) - a thought process in which knowledge of the element of the class is derived from the knowledge of the general properties of the whole class. In other words, the thought of the researcher in deduction comes from common to the private (single). For example: "All planets of the solar system are moving around the Sun"; "Planet Earth"; Consequently: "The Earth moves around the Sun." In this example, the thought is moving from the total (first parcel) to the private (output). Thus, deductive conclusion allows you to better knowly know the one, since with it, we get new knowledge (output) that this item has a sign inherent in the whole class.
The objective basis of the deduction is that each item combines the unity of the total and one. This connection is inseparable, dialectical, which allows you to learn a single knowledge of the general one. Moreover, if the parcels of deductive conclusions are true and correctly related to each other, the conclusion - the conclusion will certainly be true. This feature of the deduction is beneficial from other methods of knowledge. The fact is that the general principles and laws do not give the researcher in the process of deductive knowledge to come down from the way, they help to correctly understand the individual phenomena of real reality. However, it would be incorrectly on this basis to overestimate the scientific significance of the deductive method. After all, in order to entered into their rights, the formal power of conclusion, the original knowledge is needed, the general parcels enjoyed in the process of deduction, and their acquisition in science is a task of great complexity.
An important cognitive importance of the deduction is manifested when not just an inductive generalization acts as a common parcel, but some kind of hypothetical assumption, for example, a new scientific idea. In this case, the deduction is the starting point for the emergence of a new theoretical system. The theoretical knowledge created in this way predetermines the construction of new inductive generalizations.
All this creates real prerequisites for the steady increase in the role of deduction in a scientific study. Science is increasingly facing such objects that are not available to sensual perception (for example, a micrometer, the universe, past of humanity, etc.). As of the knowledge of this kind of objects, it is much more common to apply to the strength of thought than the strength of observation and experiment. Deduction is indispensable in all areas of knowledge, where theoretical provisions are formulated to describe formal, rather than real systems, for example, in mathematics. Since the formalization in modern science is applied more and more, the role of deduction in scientific knowledge increases accordingly.
However, the role of deduction in a scientific study cannot be absoluticized, and even more so - to oppose induction and other methods of scientific knowledge. Invalid extremes of both metaphysical and rationalistic nature. On the contrary, deduction and induction are closely interrelated and complement each other. Inductive research involves the use of general theories, laws, principles, i.e., includes the moment of deduction, and the deduction is impossible without the general provisions obtained by inductive way. In other words, induction and deduction are associated with each other as necessary as the analysis and synthesis. We must try to apply every one of them in your place, and this can be achieved only if they are not overlooked by their connection between each other, their mutual addition of each other. "Great discoveries," notes L. de Broglil, - the jumps of scientific thought are created by induction, risky, but truly creative method ... Of course, it is not necessary to conclude that the severity of deductive reasoning has no value. In fact, only It interferes with imagination of misleading, only it allows after establishing the induction of new source points to derive the investigation and compare conclusions with facts. Only one deduction can provide testing hypotheses and serve as a valuable antidote against the measure of fantasy. " With such a dialectical approach, each of the mentioned and other methods of scientific knowledge can fully show all its advantages.
Analogy. Studying properties, signs, links of objects and reality phenomena, we cannot know them immediately, entirely, in the whole volume, and we study them gradually, revealing all new and new properties step by step. After studying some of the properties of the subject, we can find that they coincide with the properties of another, already well-studied subject. Having established such similarity and finding many coinciding features, it can be assumed that other properties of these subjects also coincide. The course of such a reasoning is the basis of an analogy.
The analogy is such a method of scientific research, with which the similarity of this class objects in some signs are concluded about their similarity in other signs. The essence of the analogy can be expressed using the formula:
And has signs of AECD
In has signs of ABC
Consequently, in, apparently, has a sign D.
In other words, the thought of the researcher comes from the knowledge of the famous community to know the same community, or, in other words, from private to private.
Regarding specific objects, the findings obtained by analogy are usually only believable: they are one of the sources of scientific hypotheses, inductive reasoning and play an important role in scientific discoveries. For example, the chemical composition of the Sun is similar to the chemical composition of the Earth in many signs. Therefore, when an element of helium was found in the Sun, the element of helium was discovered, then by analogy concluded that such an element should be on Earth. The correctness of this output was established and confirmed later. Similarly, L. de Broglil, suggesting a certain similarity between the particles of the substance and the field, came to the conclusion about the wave nature of the particles of the substance.
To increase the probability of conclusions, it is necessary to strive for:
not only the external properties of compared objects were identified, and mostly internal;
these objects were similar in the most important and essential features, and not in random and secondary;
the circle of coinciding signs was as widely as possible;
not only similarity was taken into account, but also differences - to not transfer the latter to another object.
The method of an analogy gives the most valuable results when an organic relationship is established not only between similar signs, but also with that feature that is transferred to the object under study.
The truth of the conclusions can be compared with the truth of the conclusions by the method of incomplete induction. In both cases, it is possible to obtain reliable conclusions, but only when each of these methods is not isolated from other methods of scientific knowledge, but in an inseparable dialectical connection with them.
The method of an analogy, understood extremely widely, as transferring information about one objects to others, is the gnoseological basis for modeling.
Modeling - The method of scientific knowledge, with the help of which the study of the object (original) is carried out by creating its copy (model) that replaces the original, which will then know from certain parties that are interested in the researcher.
The essence of the modeling method is to reproduce the properties of the object of cognition on a specially created analogue, models. What is the model?
Model (from lat. Modulus - measure, image, norm) is a conditional image of a object (original), a certain way of expressing properties, bonds of objects and reality phenomena based on analogy, establishing similarities between them and on this basis reproduction of them On a material or ideal object - similarity. In other words, the model is an analogue, the "deputy" object of the original, which in knowledge and practice is used to acquire and expand knowledge (information) on the origin in order to design the original, transformation or management of them.
Between the model and the original there must be a known similarity (similarity ratio): physical characteristics, functions, behavior of the object being studied, its structure, etc. It is precisely this similarity and allows you to transfer information obtained as a result of a study of the model, on the original.
Since modeling has a great similarity with the analogy method, the logical structure of conclusion by analogy is as it were, as it were, the organizing factor that combines all moments of modeling into a single, targeted process. You can even say that in a certain sense, the modeling is a variety of analogy. The analogy method seems to serve as a logical basis for the conclusions that are made in modeling. For example, on the basis of the belonging of the model and the features of ABCD and accessories, the original A ABC is concluded that the property D detected in the model is also belonging to the original A.
The use of modeling is dictated by the need to reveal such parties to objects that can either be signed by directly learning, or it is unprofitable to study from purely economic considerations. A person, for example, cannot directly observe the process of natural formation of diamonds, the origin and development of life on Earth, a number of phenomena of micro and megamir. Therefore, you have to resort to artificial reproduction of such phenomena in the form, convenient for observation and study. In some cases, it is much more profitable and more economical instead of direct experimentation with the object to build and explore its model.
Modeling is widely used to calculate the trajectories of ballistic missiles, when studying the mode of operation of machines and even companies, as well as in managing enterprises, in the distribution of material resources, in the study of life processes in the body, in society.
The models used in the ordinary and scientific knowledge of the model are divided into two large classes: real, or material, and logical (mental), or ideal. The first are natural objects submitting to natural laws. They are in more or less visual form financially reproducing the subject of research. Logical models are ideal formations recorded in the appropriate sign form and functioning under the laws of logic and mathematics. The important value of the iconic models is that they use the symbols with the ability to disclose such connections and the relationship of reality that other means to detect almost impossible.
At the present stage of scientific and technological progress, computer modeling received a large distribution in science and in various fields of practice. A computer operating in a special program is able to simulate a variety of processes, for example, fluctuating of market prices, population growth, take off and exit to the orbit of an artificial satellite of the Earth, chemical reactions, etc. The study of each such process is carried out by means of an appropriate computer model.
System method . The modern stage of scientific knowledge is characterized by an increasing value of theoretical thinking and theoretical sciences. An important place among sciences occupies the theory of systems that analyzes systemic research methods. The systemic method of knowledge finds the most adequate expression of the dialectic of the development of objects and the phenomena of real reality.
The system method is a combination of general scientific methodological principles and methods of research, which is based on the orientation to disclose the integrity of the object as a system.
The basis of the system method is the system and structure that can be defined as follows.
The system (from Greek. Systema is an integer composed of parts; compound) is a general scientific position expressing the combination of elements interrelated over each other and with the medium and forming a certain integrity, the unity of the object being studied. Types of systems are very diverse: material and spiritual, inorganic and alive, mechanical and organic, biological and social, static and dynamic, etc., any system is a set of various elements that make up its defined structure. What is a structure?
Structure (from lat. Structura is a structure, location, order) - this is a relatively sustainable method (law) of the communication of the object elements, which ensures the integrity of a particular complex system.
The specificity of the system approach is determined by the fact that it focuses the study on the disclosure of the integrity of the object and ensuring its mechanisms to identify the diverse types of bonds of a complex object and minimize them into a single theoretical picture.
The basic principle of the overall theory of systems is the principle of systemic integrity, meaning the consideration of nature, including societies, as a large and complex system, disintegrating on the subsystems, protruding under certain conditions as relative to independent systems.
All the variety of concepts and approaches in the general theory of systems can be divided into two large class of theories with a certain degree of abstraction: empirical and intuitive and abstract-deductive.
1. In empirical and intuitive concepts, specific, real objects are considered as the primary object of study. In the process of climbing from a specific one, the concepts of the system and system principles of studying different levels are formulated. This method has the external similarity with the transition from one to the common in empirical knowledge, but a certain difference is hidden for external similarity. It is that if the empirical method proceeds from the recognition of the primacy of the elements, the system approach comes from the recognition of the primacy of systems. In a systematic approach, systems as a complete education consisting of a variety of elements with their relations and relations subject to certain laws are accepted as a start of research; The empirical method is limited by the formulation of laws expressing the relationship between the elements of this object or this level of phenomena. And although these laws there is a moment of generality, this commonality, however, refers to a narrow class mostly of the same names.
2. In abstract-deductive concepts, abstract objects are taken as the initial start of the study - systems characterized by extremely common properties and relationships. Further descent from extremely general systems to the increasingly accompanied by simultaneously formulating such system principles that apply to specifically specific system classes.
Empirico-intuitive and abstract-deductive approaches are equally legitimate, they are not opposed to each other, but on the contrary - their sharing opens up extremely large cognitive opportunities.
The system method allows you to scientifically interpret the principles of system organization. Objectively, the existing world acts as the world of certain systems. Such a system is characterized not only by the presence of interrelated components and elements, but also determined by their ordering, organized on the basis of a certain set of laws. Therefore, systems are not chaotic, but in a certain way ordered and organized.
In the process of research, it is possible, of course, to "go up" from elements to holistic systems, as the opposite - from holistic systems to elements. But under all circumstances, the study cannot be separated from systemic relationships and relationships. Ignoring such connections inevitably leads to one-sided or erroneous conclusions. It is not by chance that in the history of knowledge, straight and one-sided mechanism in explanation of biological and social phenomena slid on the position of the recognition of the penaltip and spiritual substance.
Based on the above, the following basic requirements of the system method can be distinguished:
Identifying the dependence of each element from its place and functions in the system, taking into account the fact that the properties of the whole are not coordinated to the sum of the properties of its elements;
Analysis of the fact that the behavior of the system is due both to the characteristics of its individual elements and the properties of its structure;
Study of the interdependence mechanism, system interaction and environment;
Study of the nature of the hierarchy inherent in this system;
Ensuring multiplicity of descriptions for the purpose of multidimensional system coverage;
Consideration of the system dynamism, representing it as a developing integrity.
An important concept of a systemic approach is the concept of "self-organization". It characterizes the process of creating, reproducing or improving the organization of a complex, open, dynamic, self-developing system, the link between the elements of which is not rigid, but probabilistic. The properties of self-organization are inherent in the objects of the most different nature: a living cell, body, biological population, human collectives.
The class of systems capable of self-organization is open and nonlinear systems. The openness of the system means the presence of sources and effluent in it, metabolism and energy with the environment. However, not any open system is self-organizing, builds structures, for it all depends on the ratio of two principles - on the basis of the creative structure, and on the basis, which dispels the beginning.
In modern science, self-organizing systems are a special subject of research of synergetics - the general scientific theory of self-organization, focused on the search for the laws of the evolution of open nonequilibrium systems of any basic basis - natural, social, cognitive (cognitive).
Currently, the system method acquires increasingly increasing methodological importance in solving natural, socially historical, psychological and other problems. It is widely used by almost all sciences, which is due to the urgent epistemological and practical needs of science development at the present stage.
Probabilistic (statistical) methods - These are such methods by which the action of a plurality of random factors characterized by a stable frequency is studied, which makes it possible to detect the need, "breaking" through the aggregate action of a plurality of accidents.
Probability methods are formed on the basis of the theory of probability, which is often called science on random, and in the presentation of many scientists the likelihood and randomness of practically unborn. The categories of need and chance are not outdated, on the contrary - their role in modern science has increased immeasurably. As the history of knowledge showed, "we are just now begin to appreciate the importance of the whole range of problems related to necessity and chance."
To understand the substance of probabilistic methods, it is necessary to consider their basic concepts: "dynamic patterns", "statistical patterns" and "probability". The two types of patterns differ in the nature of predictions arising from them.
The laws of a dynamic type of prediction are definite. Dynamic laws characterize the behavior of the relatively isolated objects consisting of a small number of elements in which you can abstract from a variety of random factors, which creates more accurately predict, for example, in classical mechanics.
In statistical laws, prediction are not reliable, but only probabilistic. This nature of the predictions is due to the action of a set of random factors that occur in statistical phenomena or mass events, for example, a large number of gas molecules, the number of individuals in populations, the number of people in large groups, etc.
Statistical pattern arises as a result of the interaction of a large number of elements that make up the object - the system, and therefore does not characterize the behavior of the individual element as the object as a whole. The need manifested in statistical laws arises due to mutual compensation and balancing the set of random factors. "Although statistical patterns and can lead to allegations, the degree of probability of which is so high that it borders with reliability, nevertheless, exceptions are always possible."
Statistical laws, although they do not give unequivocal and reliable predictions, however, are the only possible in the study of massive phenomena of a random nature. For the cumulative action of various random factors, which are almost impossible to embrace, statistical laws are detected by something sustainable required, repeated. They serve as confirmation of the dialectic of the transition of the random to the necessary one. Dynamic laws turn out to be an extreme case of statistical when the probability becomes practically reliable.
The probability is a notion characterizing the quantitative measure (degree) of the possibility of the appearance of a certain random event under certain conditions that can repeatedly repeat. One of the main tasks of probability theory is to determine the patterns arising from the interaction of a large number of random factors.
Probability statistical methods are widely used in the study of mass phenomena, especially in such scientific disciplines such as mathematical statistics, statistical physics, quantum mechanics, cybernetics, synergetics.
3.5.1. Probabilistic statistical research method.
In many cases, it is necessary to investigate not only deterministic, but also random probabilistic (statistical) processes. These processes are discussed on the basis of probability theory.
The combination of the random variable is the primary mathematical material. A set of many homogeneous events understand. A combination containing the most different variants of the mass phenomenon is called the general population, or big sample N.Typically, only part of the general population called electoral set or small sample.
Probability P (x)events h.call the attitude of the number of cases N (x),which lead to events h.to the total number of possible cases N:
P (x) \u003d n (x) / n.
Probability theoryconsiders the theoretical distributions of random variables and their characteristics.
Math statisticsengaged in the methods of processing and analyzing empirical events.
These two related sciences constitute a single mathematical theory of mass random processes, widely used to analyze scientific research.
Very often used methods of probabilities and mathematical statistics in the theory of reliability, survivability and security, which is widely used in various industries of science and technology.
3.5.2. Method of statistical modeling or statistical tests (Monte Carlo method).
This method is a numerical method of solving complex tasks and is based on the use of random numbers that simulate probabilistic processes. The results of the solution by this method allow you to establish empirically dependence of the processes under study.
The problem solving by Monte Carlo is effectively using high-speed computer. To solve problems by Monte Carlo, it is necessary to have a statistical number, to know the law of its distribution, the average mathematical expectation t (x),radant deviation.
With this method, it is possible to obtain an arbitrarily specified accuracy of the solution, i.e.
-\u003e T (x)
3.5.3. System analysis method.
Under system analysis, a set of techniques and methods understand for the study of complex systems, which are a complex combination of elements interacting with each other. The interaction of the elements of the system is characterized by direct and inverse relations.
The essence of the system analysis is to identify these links and establish their effect on the behavior of the entire system as a whole. The most fully and deeply can be performed by system analysis by cybernetics methods, which is a science of complex dynamic systems that can perceive, store and recycle information for optimization and control purposes.
Systemic analysis is made up of four stages.
The first stage is to formulate the problem: the object, objectives and objectives of the study, as well as the criteria for studying the object and management of them are determined.
During the second stage, the boundaries of the system studied and determine its structure. All objects and processes related to the goal are divided into two classes ~ actually studied system and external environment. Distinguish closedand opensystems. In the study of closed systems with the influence of the external environment, their behavior is neglected. Then the individual components of the system are isolated - its elements, set the interaction between them and the external environment.
The third stage of the system analysis is to compile a mathematical model of the system under study. Initially, the system parameterization is performed, describe the main elements of the system and elementary effects on it using certain parameters. In this case, the parameters characterizing continuous and discrete, deterministic and probabilistic processes are distinguished. Depending on the characteristics of the processes, one or no mathematical apparatus is used.
As a result of the third stage of the system analysis, complete mathematical models of the system described on the formal, for example, algorithmic, language are formed.
At the fourth stage, the resulting mathematical model is analyzed, its extreme conditions are found in order to optimize processes and management of systems and formulate conclusions. An optimization estimate is made by the criterion of optimization that takes extreme values \u200b\u200bin this case (minimum, maximum, minimax).
Usually choose any one criterion, and for others, the thresholds of extreme-permissible values \u200b\u200bare installed. Sometimes mixed criteria are used, which are function from primary parameters.
Based on the selected optimization criterion, the dependence of the optimization criterion from the parameters of the model of the object under study (process) is constituted.
Various mathematical methods of optimization of the studied models are known: methods of linear, nonlinear or dynamic programming; Methods are probabilistic-statistical, based on mass maintenance theory; The theory of games that considers the development of processes as random situations.
Questions for self-controlling knowledge
Methodology of theoretical studies.
The main sections of the stage of theoretical developments of scientific research.
Types of models and types of modeling of the object of the study.
Analytical research methods.
Analytical research methods using the experiment.
Probabilically analytical research method.
Static modeling methods (Monte Carlo method).
Method of system analysis.
The considered group of methods is the most important in sociological studies, these methods are applied in almost every sociological study, which can be considered truly scientific. They are directed mainly to identifying statistical laws in empirical information, i.e. Laws running "on average". Actually, sociology and is engaged in the study of the "middle man". In addition, another important goal of the application of probabilistic and statistical methods in sociology is an assessment of the reliability of the sample. How big is the confidence that the sample gives more or less accurate results and what is the error of statistical conclusions?
The main object of study when applying probabilistic and statistical methods - random variables. The acceptance of a random value of some value is random event - An event that, when making these conditions, can occur how to happen and not happen. For example, if a sociologist conducts polls in the field of political preferences on the street of the city, the event "the next respondent turned out to be a supporter of the party of power" is random, if nothing in the respondent did not give it to political preference in advance. If the sociologist interviewed the respondent at the building of the regional Duma, the event is no longer accidental. Random event is characterized probability His offensive. Unlike classical tasks on playing bones and card combinations studied within the framework of the course of probability theory, in sociological studies, it is not so easy to calculate the likelihood.
The most important basis for the empirical assessment of the probability is the desire of frequency to probabilityIf the relationship is under the frequency, how many times the event happened to how many times it couldoretically occur. For example, if the respondents' respondents were randomly selected on the streets of the city of respondents 220, the frequency of such respondents is 0.44. When representative sampling sufficiently large We will get an exemplary chance of an event or an approximate share of people with a given feature. In our example, with a well-selected sample, we obtain that approximately 44% of citizens - supporters of the party of power. Of course, since there are not all citizens, and some in the survey process could lie, then there is some error.
Consider some tasks arising from statistical analysis of empirical data.
Estimation of the distribution of magnitude
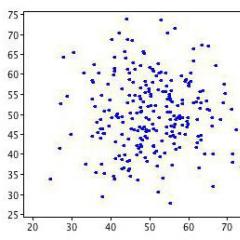
If some feature can be quantified (for example, the political activity of a citizen as a magnitude showing how many times over the past five years he participated in the elections of a different level), then the task may be set to assess the law of the distribution of this feature as a random variable. In other words, the distribution law shows which values \u200b\u200bvalue takes more often, and what less often, and how much more often. Most often both in the technique and nature, and in society meets normal distribution law . Its formula and properties are set out in any textbook on statistics, and in Fig. 10.1 The type of graphics is a "bell-shaped" curve that can be more "elongated" up or more "smeared" along the axis of random variance values. The essence of a normal law is that most often a random value takes values \u200b\u200bnear some "central" meaning called mathematical expectationAnd the farther from him, the less often "falls" the value.
Examples of distributions that can be taken for normal with a small error. Back in the XIX century. Belgian scientist A. Ketle and Englishman F. Galton proved that the distribution of frequencies of the occurrence of any demographic or anthropometric indicator (life expectancy, growth, age of marriage, etc.) is characterized by the "bell-shaped" distribution. The same F. Galton and his followers proved that both psychological wellms, for example, the ability, obey the normal law.
Fig. 10.1.
Example
The most vivid example of a normal distribution in sociology concerns the social activity of people. According to the law of the normal distribution, it turns out that socio-active people in society are usually about 5-7%. All these socio-active people go to rallies, conferences, seminars, etc. Approximately the same amount is generally removed from participation in social life. The bulk of people (80-90%) seems to be indifferent to politics and public life, but tracks those processes that they are interesting, although generally relates to politics and society removed, there is no significant activity. Such people skip most political events, but from time to time they watch news on television or on the Internet. They also go to vote on the most important elections, especially if they "threaten the whip" or "encourage the gingerbread". The members of these 80-90% from a socio-political point of view are almost useless one, but these people are quite interesting to the centers of sociological studies, as they are very much, and their preferences cannot be ignored. The same applies to the occasional organizations that perform research on orders of political figures or trade corporations. And the opinion of the "gray mass" on key issues related to the prediction of the behavior of many thousands and millions of people in elections, as well as with acute political events, with a split society and conflicts of different political forces, are not indifferent to these centers.
Of course, the NS are all values \u200b\u200bare distributed according to normal distribution. In addition to him, the most important in mathematical statistics are the binomial and indicative distribution, the distribution of Fisher-Sandecore, "Chi-Square", Student.
Evaluation of communication signs
The simplest case - when you need to simply establish the presence / lack of communication. The most popular in this question is the "Chi-Square" method. This method is focused on working with categorical data. For example, the floor, marital status, are clearly performed. Some data at first glance seem numeric, but can "turn out" into categorical by splitting the interval of values \u200b\u200binto several small intervals. For example, work experience at the factory can be divided into categories "less than one year", "from one to three years", "from three to six years" and "more than six years."
Let the parameter X. Available p Possible values: (x1, ..., h.g1), and at the parameter Y- T. Possible values: (u1, ..., w.t) , Q.ij - the observed frequency of the appearance of a pair ( x.i, w.j), i.e. The number of discovered appearances of such a pair. Calculate theoretical frequencies, i.e. How many times each pair of values \u200b\u200bshould appear for absolutely related values \u200b\u200bof themselves:

Based on the observed and theoretical frequencies, calculate the value
![]()
Also required to calculate the number degrees of freedom according to the formula
![]()
where m., n. - The number of categories reduced into the table. In addition, choose significance level. The higher reliability We want to get, the lower the level of significance should be taken. As a rule, a value of 0.05 is selected, which means that we can trust the results with a probability of 0.95. Further, in reference tables, we find the number of degrees of freedom and the level of significance critical value. If, then the parameters X. and Y. considered independent. If, then the parameters X. and Y - dependent. If, it is dangerous to make a conclusion about the dependence of either the independence of the parameters. In the latter case, it is advisable to carry out additional research.
We also note that the criterion "chi-square" with very high confidence can be used only when all theoretical frequencies are not lower than the specified threshold, which is usually considered to be 5. Let v be the minimum theoretical frequency. When V\u003e 5, you can confidently use the criterion "chi-square". With V.< 5 использование критерия становится нежелательным. При v ≥ 5 вопрос остается открытым, требуется дополнительное исследование о применимости критерия "Хи-квадрат".
Let us give an example of the use of the "Chi-Square" method. Let, for example, in a certain city, a survey was conducted among young fans of local football teams and the following results were obtained (Table 10.1).
Put forward the hypothesis about the independence of the football preferences of the city of the city N. From the floor of the respondent at the standard level of significance 0.05. Calculate theoretical frequencies (Table 10.2).
Table 10.1.
The results of the survey of fans
Table 10.2.
Theoretical frequencies of preferences
For example, the theoretical frequency for young-fans of the star was obtained as
similarly - other theoretical frequencies. Next, we calculate the value of "chi-square":

Determine the number of degrees of freedom. For and levels of significance 0.05 We are looking for a critical value:
Since, and the superiority is essential, almost certainly you can say that the football preferences of the boys and girls of the city N. Easily vary, except for the incidental sample case, for example, if the researcher did not receive a sample from different parts of the city, restricted by the survey of respondents in his quarter.
A more complex situation - when you need to quantify the connection force. In this case, methods often apply correlation analysis.These methods are usually considered in the in-depth courses of mathematical statistics.
Approximation of dependencies on point data
Let there be a set of points - empirical data ( X.i, Yi), i. = 1, ..., p. It is required to approximate the real dependence of the parameter. w. from the parameter x, and develop a rule calculation rule y, when h. Located between two "nodes" xi.
There are two fundamentally different approaches to solving the task. The first is that among the functions of a given family (for example, polynomials), a function is selected, the graph of which passes through the available points. The second approach does not "force" the schedule of the function to pass through the points. Most popular in sociology and a number of other sciences method - least square method - refers to the second group of methods.
The essence of the least squares method is as follows. Given some family of functions w.(x, A.1, ..., butt) S. m. uncertain coefficients. It is required to choose uncertain coefficients by solving the optimization task.
Minimum function value d. May act as a measure of accuracy of approximation. If this value is too large, you should select another class of functions w. Or expand the used class. For example, if the class of "polynomials is no higher than 3" did not give acceptable accuracy, we take the class "polynomials no higher than 4" or even "polynomials no higher than 5".
Most often, the method is used for the family "polynomials no higher N ":
For example, as N. \u003d 1 is a family of linear functions, with N \u003d 2 - Family of linear and quadratic functions, with N \u003d 3 - Family of linear, quadratic and cubic functions. Let be
Then the coefficients of the linear function ( N. \u003d 1) are searched as a solution of a system of linear equations
The coefficients of the type of type but0 + A.1x + A.2h.2 (N \u003d 2) are looking for as a solution system

![]()

Those who want to apply this method for arbitrary value N. These can do this, seeing the pattern according to which the presented systems of equations are compiled.
We give an example of the application of the least squares method. Let the number of some political party changed as follows:
It can be noted that the change in the number of the party for different years is not very different, which allows us to approximate the dependence of the linear function. To make it easier to calculate, instead of a variable h. - year - we introduce a variable t \u003d x - 2010, i.e. The first year of accounting is taking into account as "zero". Calculate M.1; M.2:
Now we calculate M ", M *:
Factors a.0, a.1 Functions y \u003d A.0t. + but1 are calculated as a solution system of equations
![]()
Solving this system, for example, by the rules of the craver or the substitution method, we obtain: but0 = 11,12; but1 \u003d 3.03. Thus, we get the approach
which allows not only to operate with one function instead of a set of empirical points, but also calculate the values \u200b\u200bof the function that go beyond the boundaries of the source data is "predicting the future".
We also note that the least squares method can be used not only for polynomials, but also for other families of functions, for example, for logarithms and exponentials:
The degree of reliability of the model built on the basis of the least squares method can be determined based on the measure "R-square" or the determination coefficient. It is calculated as
![]()
Here ![]() . The closer R.2 to 1, the more adequately model.
. The closer R.2 to 1, the more adequately model.
Detection of emissions
The emission of a number of data is an abnormal value, dramatically released in a general sample or a general row. For example, let the percentage of citizens of the country positively relating to some policies amounted to in 2008-2013. Accordingly, 15, 16, 12, 30, 14 and 12%. It is easy to see that one of the values \u200b\u200bis sharply different from all others. In 2011, the rating of the policy for some reason sharply exceeded the usual values \u200b\u200bheld in the range of 12-16%. The presence of emissions may be due to different reasons:
- 1) Measurement errors;
- 2) unusual input nature(for example, when an average percentage of votes received by a politician are analyzed; this value at the polling station in the military unit can differ significantly from the average city);
- 3) corollary(sharply different from the remaining values \u200b\u200bmay be due to mathematical law - for example, in the case of a normal distribution, an object with a value, sharply different from the average), may fall into the sample);
- 4) cataclysm(for example, in a short, but acute political confrontation period, the level of political activity of the population may change dramatically, as happened during the "color revolutions" 2000-2005 and the "Arab Spring" 2011);
- 5) control impact(For example, if in the year on the eve of the policy of policies accepted a very popular decision, then this year its rating may be significantly higher than in other years).
Many methods of data analysis are unstable to emissions, so you need to clean data from emissions to effectively use. A vivid example of an unstable method is the above-mentioned method of smallest squares. The simplest method of finding emissions is based on the so-called emerquartered distance.Determine the range
where Q.m. – value t-th ped. If some member of the row does not fall into the range, then it is regarded as an emission.
Let us explain on the example. The meaning of quarters is that they share a number of four equal or approximately equal groups: the first apartment "separates" the left quarter of a row, sorted by increasing, the third quartile is the right quarter of a number, the second apartment passes in the middle. Explain how to search Q.1, I. Q.3. Let in the numerical row sorted by increasing p values. If a p + 1 is divided by 4 without a residue, then Q.k essence k.(p + 1) / 4th member of the row. For example, a row is available: 1, 2, 5, 6, 7, 8, 10, 11, 13, 15, 20, here the number of members n \u003d 11. Then ( p + 1) / 4 \u003d 3, i.e. First quarters Q.1 \u003d 5 - the third member of the row; 3 ( p + 1) / 4 \u003d 9, i.e. Third quartile Q: I \u003d 13 - ninth member of a number.
A little more difficult case when p + 1 Not multiple 4. For example, a range of 2, 3, 5, 6, 7, 8, 9, 30, 32, 100, where the number of members p \u003d 10. Then ( p + 1)/4 = 2,75 -
the position between the second member of the series (V2 \u003d 3) and the third member of the series (V3 \u003d 5). Then we take the value of 0.75v2 + 0.25v3 \u003d 0.75 3 + 0.25 5 \u003d 3.5 - it will be Q.1. 3(p + 1) / 4 \u003d 8.25 - position between the eighth member of the row (V8 \u003d 30) and the ninth member of the series (V9 \u003d 32). We take a value of 0.25v8 + 0.75v9 \u003d 0.25 30 + + 0.75 32 \u003d 31.5 - it will be Q.3. There are other calculation options. Q.1 I. Q.3, but it is recommended to use the option outlined here.
- Strictly speaking, in practice it is usually found "approximately" a normal law - since the normal law is determined for the continuous magnitude on the entire valid axis, many real values \u200b\u200bcannot strictly satisfy the properties of normally distributed values.
- Hrenov A. D. Mathematical methods of psychological research. Analysis and interpretation of data: studies, benefit. SPb.: Speech, 2004. P. 49-51.
- On the most important distributions of random variables, see, for example: Orlov A. I. Mathematics Case: Probability and Statistics - Basic Facts: Proc. benefit. M.: MH-Press, 2004.