Різні способи доказу теореми Піфагора: приклади, опис та відгуки. Як застосовувати теорему піфагора Піфагора

теорема Піфагора- Одна з основних теорем евклідової геометрії, що встановлює співвідношення

між сторонами прямокутного трикутника.

Вважається, що доведено грецьким математиком Піфагором, на честь якого названо.

Геометричне формулювання теореми Піфагора.

Спочатку теорема була сформульована наступним чином:

У прямокутному трикутнику площа квадрата, побудованого на гіпотенузі, дорівнює сумі площ квадратів,

побудованих на катетах.

Алгебраїчне формулювання теореми Піфагора.

У прямокутному трикутнику квадрат довжини гіпотенузи дорівнює сумі квадратів довжин катетів.

Тобто, позначивши довжину гіпотенузи трикутника через c, а довжини катетів через aі b:

Обидві формулювання теореми Піфагораеквівалентні, але друге формулювання більш елементарне, воно не

потребує поняття площі. Тобто друге твердження можна перевірити, нічого не знаючи про площу та

вимірявши тільки довжини сторін прямокутного трикутника.

Зворотний теорема Піфагора.

Якщо квадрат однієї сторони трикутника дорівнює сумі квадратів двох інших сторін, то

трикутник прямокутний.

Або, іншими словами:

Для будь-якої трійки позитивних чисел a, bі c, такий, що

існує прямокутний трикутник із катетами aі bта гіпотенузою c.

Теорема Піфагора для рівнобедреного трикутника.

Теорема Піфагор для рівностороннього трикутника.

Докази теореми Піфагора.

На даний момент у науковій літературі зафіксовано 367 доказів цієї теореми. Ймовірно, теорема

Піфагора є єдиною теоремою з настільки значним числом доказів. Таке різноманіття

можна пояснити лише фундаментальним значенням теореми для геометрії.

Зрозуміло, концептуально їх можна розбити на малу кількість класів. Найвідоміші з них:

докази методом площ, аксіоматичніі екзотичні докази(наприклад,

за допомогою диференціальних рівнянь).

1. Доказ теореми Піфагора через трикутники.

Наступний доказ алгебраїчного формулювання - найпростіший з доказів, що будуються

безпосередньо з аксіом. Зокрема воно не використовує поняття площі фігури.

Нехай ABCє прямокутний трикутник із прямим кутом C. Проведемо висоту з Cі позначимо

її заснування через H.

Трикутник ACHподібний до трикутника ABЗ двома кутами. Аналогічно трикутник CBHподібний ABC.

Ввівши позначення:

отримуємо:

що відповідає -

Склавши a 2 та b 2, отримуємо:

або , що потрібно було довести.

2. Підтвердження теореми Піфагора шляхом площ.

Нижче наведені докази, незважаючи на їхню простоту, зовсім не такі прості. Всі вони

використовують властивості площі, докази яких складніші за доказ самої теореми Піфагора.

Доказ через рівнодоповнюваність.

Розташуємо чотири рівні прямокутні

трикутника так, як показано на малюнку

праворуч.

Чотирикутник зі сторонами c- Квадратом,

оскільки сума двох гострих кутів 90°, а

розгорнутий кут - 180 °.

Площа всієї фігури дорівнює, з одного боку,

площі квадрата зі стороною ( a+b), а з іншого боку, сумі площ чотирьох трикутників і

Що й потрібно було довести.

3. Доказ теореми Піфагора методом нескінченно малих.

Розглядаючи креслення, показане на малюнку, і

спостерігаючи зміну сторониa, ми можемо

записати наступне співвідношення для нескінченно

малих прирощень сторінзі a(використовуючи подобу

трикутників):

Використовуючи метод поділу змінних, знаходимо:

Більш загальний вираз зміни гіпотенузи у разі прирощень обох катетів:

Інтегруючи дане рівняння та використовуючи початкові умови, отримуємо:

Таким чином, ми приходимо до бажаної відповіді:

Як неважко бачити, квадратична залежність у остаточній формулі з'являється завдяки лінійній

пропорційності між сторонами трикутника та прирощеннями, тоді як сума пов'язана з незалежними

вкладами від збільшення різних катетів.

Простіший доказ можна отримати, якщо вважати, що один з катетів не відчуває збільшення

(в даному випадку катет b). Тоді для константи інтегрування отримаємо:

На думку Ван-дер-Вардена, дуже ймовірно, що співвідношення в загальному вигляді було відоме у Вавилоні вже близько XVIII-століття до н. е.

Приблизно 400 року до зв. е., згідно з Проклом, Платон дав метод знаходження піфагорових трійок, що поєднує алгебру та геометрію. Близько 300 року до зв. е. в «Початках» Евкліда з'явився найстаріший аксіоматичний доказ теореми Піфагора.

Формулювання

Основне формулювання містить алгебраїчні дії - у прямокутному трикутнику, довжини катетів якого рівні a (\displaystyle a)і b (\displaystyle b), а довжина гіпотенузи - c (\displaystyle c), Виконано співвідношення:

Можливе і еквівалентне геометричне формулювання, що вдається до поняття площі фігури: у прямокутному трикутнику площа квадрата, побудованого на гіпотенузі, дорівнює сумі площ квадратів, побудованих на катетах. У такому вигляді теорема сформульована на Початках Евкліда.

Зворотня теорема Піфагора- твердження про прямокутність будь-якого трикутника, довжини сторін якого пов'язані співвідношенням a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)). Як наслідок, для будь-якої трійки позитивних чисел a (\displaystyle a), b (\displaystyle b)і c (\displaystyle c), такий, що a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2))існує прямокутний трикутник з катетами a (\displaystyle a)і b (\displaystyle b)та гіпотенузою c (\displaystyle c).

Докази

У науковій літературі зафіксовано щонайменше 400 доказів теореми Піфагора, що як фундаментальним значенням для геометрії, і елементарністю результату. Основні напрями доказів: використання алгебри співвідношень елементів-трикутника (таких, наприклад, популярний метод подібності ), метод площ , існують також різні екзотичні докази (наприклад, за допомогою диференціальних рівнянь).

Через подібні трикутники

Класичний доказ Евкліда спрямовано встановлення рівності площ між прямокутниками, утвореними з розтину квадрата над гіпотенузою висотою із прямого кута з квадратами над катетами.

Конструкція, яка використовується для доказу: для прямокутного трикутника з прямим кутом C (\displaystyle C), квадратів над катетами та квадрата над гіпотенузою A B I K (\displaystyle ABIK)будується висота C H (\displaystyle CH)і промінь, що її продовжує, s (\displaystyle s), що розбиває квадрат над гіпотенузою на два прямокутники і . Доказ націлений на встановлення рівності площ прямокутника A H J K (\displaystyle AHJK)з квадратом над катетом A C (\displaystyle AC); рівність площ другого прямокутника, що становить квадрат над гіпотенузою, та прямокутника над іншим катетом встановлюється аналогічним чином.

Рівність площ прямокутника A H J K (\displaystyle AHJK)і A C E D (\displaystyle ACED)встановлюється через конгруентність трикутників △ A C K (\displaystyle \triangle ACK)і △ A B D (\displaystyle \triangle ABD)площа кожного з яких дорівнює половині площі квадратів. A H J K (\displaystyle AHJK)і A C E D (\displaystyle ACED)відповідно у зв'язку з наступною властивістю: площа трикутника дорівнює половині площі прямокутника, якщо фігур є спільна сторона, а висота трикутника до загальної сторони є іншою стороною прямокутника. Конгруентність трикутників випливає з рівності двох сторін (сторони квадратів) та куту між ними (складеного з прямого кута і кута при A (\displaystyle A).

Таким чином, доказом встановлюється, що площа квадрата над гіпотенузою, що складається з прямокутників A H J K (\displaystyle AHJK)і B H J I (\displaystyle BHJI), що дорівнює сумі площ квадратів над катетами.

Доказ Леонардо да Вінчі

До методу площ належить також доказ, знайдений Леонардо да Вінчі. Нехай дано прямокутний трикутник △ A B C (\displaystyle \triangle ABC)з прямим кутом C (\displaystyle C)та квадрати A C E D (\displaystyle ACED), B C F G (\displaystyle BCFG)і A B H J (\displaystyle ABHJ)(Див. малюнок). У цьому доказі на стороні H J (\displaystyle HJ)останнього у зовнішній бік будується трикутник, конгруентний △ A B C (\displaystyle \triangle ABC), до того ж відбитий як щодо гіпотенузи, і щодо висоти до неї (тобто J I = B C (\displaystyle JI = BC)і H I = A C (\displaystyle HI=AC)). Пряма C I (\displaystyle CI)розбиває квадрат, побудований на гіпотенузі на дві рівні частини, оскільки трикутники △ A B C (\displaystyle \triangle ABC)і △ J H I (\displaystyle \triangle JHI)рівні з побудови. Доказ встановлює конгруентність чотирикутників C A J I (\displaystyle CAJI)і D A B G (\displaystyle DABG), площа кожного з яких, виявляється, з одного боку, дорівнює сумі половин площ квадратів на катетах і площі вихідного трикутника, з іншого боку - половині площі квадрата на гіпотенузі плюс площа вихідного трикутника. Отже, половина суми площ квадратів над катетами дорівнює половині площі квадрата над гіпотенузою, що дорівнює геометричному формулюванню теореми Піфагора.

Доказ методом нескінченно малих

Існує кілька доказів, що вдаються до техніки диференціальних рівнянь. Зокрема, Харді приписується доказ, який використовує нескінченно малі прирощення катетів. a (\displaystyle a)і b (\displaystyle b)та гіпотенузи c (\displaystyle c)і зберігають подібність з вихідним прямокутником, тобто, що забезпечують виконання наступних диференціальних співвідношень:

d a d c = c a (displaystyle (frac (da) (dc)) = (frac (c) (a))), d b d c = c b (displaystyle (frac (db) (dc)) = (frac (c) (b))).

Методом поділу змінних їх виводиться диференціальне рівняння c d c = a d a + b d b (displaystyle c dc = a, da + b, db), інтегрування якого дає співвідношення c 2 = a 2 + b 2 + C o ns t (\displaystyle c^(2)=a^(2)+b^(2)+\mathrm (Const) ). Застосування початкових умов a = b = c = 0 (\displaystyle a=b=c=0)визначає константу як 0, що у результаті дає затвердження теореми.

Квадратична залежність у остаточній формулі з'являється завдяки лінійній пропорційності між сторонами трикутника та прирощеннями, тоді як сума пов'язана з незалежними вкладами від прирощення різних катетів.

Варіації та узагальнення

Подібні геометричні фігури на трьох сторонах

Важливе геометричне узагальнення теореми Піфагора дав Евклід в "Початках", перейшовши від площ квадратів на сторонах до площ довільних подібних геометричних фігур: сума площ таких фігур, побудованих на катетах, дорівнюватиме площі подібної їм фігури, побудованої на гіпотенузі.

Головна ідея цього узагальнення полягає в тому, що площа подібної геометричної фігури є пропорційною квадрату будь-якого свого лінійного розміру і зокрема квадрату довжини будь-якої сторони. Отже, для подібних фігур із майданами A (\displaystyle A), B (\displaystyle B)і C (\displaystyle C), побудованих на катетах із довжинами a (\displaystyle a)і b (\displaystyle b)та гіпотенузі c (\displaystyle c)відповідно, має місце співвідношення:

A a 2 = B b 2 = C c 2 ⇒ A + B = a 2 c 2 C + b 2 c 2 C (displaystyle (frac (A)(a^(2))))=(frac (B )(b^(2)))=(\frac (C)(c^(2)))\,\Rightarrow \,A+B=(\frac (a^(2))(c^(2) ))C+(\frac (b^(2))(c^(2)))C).

Бо за теоремою Піфагора a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)), то виконано.

Крім того, якщо можна довести без залучення теореми Піфагора, що для площ трьох подібних геометричних фігур на сторонах прямокутного трикутника виконано співвідношення A + B = C (\displaystyle A+B=C), то з використанням зворотного ходу підтвердження узагальнення Евкліда можна вивести підтвердження теореми Піфагора. Наприклад, якщо на гіпотенузі побудувати конгруетний початковий прямокутний трикутник площею C (\displaystyle C), а на катетах - два подібні йому прямокутні трикутники з площами A (\displaystyle A)і B (\displaystyle B), то виявляється, що трикутники на катетах утворюються в результаті розподілу початкового трикутника його висотою, тобто сума двох менших площ трикутників дорівнює площі третього, таким чином A + B = C (\displaystyle A+B=C)і, застосовуючи співвідношення для таких фігур, виводиться теорема Піфагора.

Теорема косінусів

Теорема Піфагора - це окремий випадок більш загальної теореми косінусів, яка пов'язує довжини сторін у довільному трикутнику:

a 2 + b 2 − 2 a b cos ⁡ θ = c 2,

де - кут між сторонами a (\displaystyle a)і b (\displaystyle b). Якщо кут дорівнює 90 °, то cos ⁡ θ = 0 (\displaystyle \cos \theta =0)і формула спрощується до звичайної теореми Піфагора.

Довільний трикутник

Існує узагальнення теореми Піфагора на довільний трикутник, що оперує виключно співвідношенням довжин сторін, вважається, що воно вперше було встановлено сабійським астрономом Сабітом Ібн Куррою. У ньому для довільного трикутника зі сторонами до нього вписується рівнобедрений трикутник з основою на стороні c (\displaystyle c), вершиною, що збігається з вершиною вихідного трикутника, що протилежить стороні c (\displaystyle c)і кутами при підставі, рівними куту θ (\displaystyle \theta), протилежному боці c (\displaystyle c). У результаті утворюються два трикутники, подібні до вихідного: перший - зі сторонами a (\displaystyle a), далекою від неї бічною стороною вписаного рівнобедреного трикутника, та r (\displaystyle r)- частини сторони c (\displaystyle c); другий - симетрично до нього від боку b (\displaystyle b)зі стороною s (\displaystyle s)- відповідною частиною сторони c (\displaystyle c). В результаті виявляється виконане співвідношення:

a 2 + b 2 = c (r + s) (\displaystyle a (2) + b (2) = c (r + s)),

що вироджується в теорему Піфагора при θ = π / 2 (\displaystyle \theta =\pi /2). Співвідношення є наслідком подібності утворених трикутників:

c a = a r , c b = b s ⇒ c r + c s = a 2 + b 2 (displaystyle (frac (c)(a))=(frac (a)(r)),\,(\frac (c) (b))=(\frac (b)(s))\,\Rightarrow \,cr+cs=a^(2)+b^(2)).

Теорема Паппа про площі

Неєвклідова геометрія

Теорема Піфагора виводиться з аксіом евклідової геометрії і недійсна для неевклідової геометрії - виконання теореми Піфагора рівносильне постулату Евкліда паралельності.

У неевклідовій геометрії співвідношення між сторонами прямокутного трикутника обов'язково буде у формі, яка відрізняється від теореми Піфагора. Наприклад, у сферичній геометрії всі три сторони прямокутного трикутника, які обмежують собою октант одиничної сфери, мають довжину π / 2 (\displaystyle \pi /2), що суперечить теоремі Піфагора

При цьому теорема Піфагора справедлива в гіперболічній та еліптичній геометрії, якщо вимогу про прямокутність трикутника замінити умовою, що сума двох кутів трикутника повинна дорівнювати третьому.

Сферична геометрія

Для будь-якого прямокутного трикутника на сфері радіусом R (\displaystyle R)(наприклад, якщо кут у трикутнику прямий) зі сторонами a, b, c (\displaystyle a, b, c)співвідношення між сторонами має вигляд:

cos ⁡ (c R) = cos ⁡ (a R) ⋅ cos ⁡ (b R) (\displaystyle \cos \left((\frac(c)(R))\right)=\cos \left((\frac) (a)(R))\right)\cdot \cos \left((\frac (b)(R))\right)).

Ця рівність може бути виведена як особливий випадок сферичної теореми косинусів, яка справедлива для всіх сферичних трикутників:

cos ⁡ (c R) = cos ⁡ (a R) ⋅ cos ⁡ (b R) + sin ⁡ (a R) ⋅ sin ⁡ (b R) ⋅ cos ⁡ γ (\displaystyle \cos \left((\frac ( c)(R))\right)=\cos \left((\frac (a)(R))\right)\cdot \cos \left((\frac (b)(R))\right)+\ sin \left((\frac (a)(R))\right)\cdot \sin \left((\frac(b)(R))\right)\cdot \cos \gamma ). ch ⁡ c = ch ⁡ a ⋅ ch ⁡ b (\displaystyle \operatorname(ch) c=\operatorname (ch),

де ch (\displaystyle \operatorname (ch) )- Гіперболічний косинус. Ця формула є окремим випадком гіперболічної теореми косінусів, яка справедлива для всіх трикутників:

ch ⁡ c = ch ⁡ a ⋅ ch ⁡ b − sh ⁡ a ⋅ sh ⁡ b ⋅ cos ⁡ γ (\displaystyle \operatorname(ch) c=\operatorname (ch) a\cdot \operatorname (ch) (sh) a\cdot \operatorname (sh) b\cdot \cos \gamma ),

де γ (\displaystyle \gamma)- Кут, вершина якого протилежна стороні c (\displaystyle c).

Використовуючи ряд Тейлора для гіперболічного косинуса ( ch ⁡ x ≈ 1 + x 2 / 2 (\displaystyle \operatorname (ch) x\approx 1+x^(2)/2)) можна показати, що якщо гіперболічний трикутник зменшується (тобто коли a (\displaystyle a), b (\displaystyle b)і c (\displaystyle c)прагнуть до нуля), то гіперболічні співвідношення у прямокутному трикутнику наближаються до співвідношення класичної теореми Піфагора.

Застосування

Відстань у двовимірних прямокутних системах

Найважливіше застосування теореми Піфагора - визначення відстані між двома точками у прямокутній, системі, координат: відстань s (\displaystyle s)між точками з координатами (a, b) (\displaystyle (a,b))і (c, d) (\displaystyle (c,d))одно:

s = (a − c) 2 + (b − d) 2 (\displaystyle s=(\sqrt ((a-c)^(2)+(b-d)^(2)))).

Для комплексних чисел теорема Піфагора дає природну формулу для знаходження модуля комплексного числа - для z = x + y i (\displaystyle z = x + yi)він дорівнює довжині

Теорема

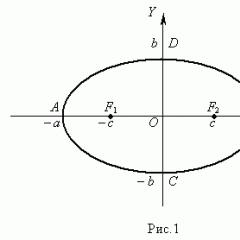
У прямокутному трикутнику квадрат довжини гіпотенузи дорівнює сумі квадратів довжин катетів (рис. 1):

$c^(2)=a^(2)+b^(2)$

Доказ теореми Піфагора

Нехай трикутник $A B C$ - прямокутний трикутник із прямим кутом $C$ (рис. 2).

Проведемо висоту з вершини $ C $ на гіпотенузу $ A B $, основу висоти позначимо як $ H $.

Прямокутний трикутник $A C H$ подібний до трикутника $A B C$ по двох кутах ($\angle A C B=\angle C H A=90^(\circ)$, $\angle A$ - загальний). Аналогічно, трикутник $C B H$ подібний до $A B C$ .

Ввівши позначення

$$B C=a, A C=b, A B=c$$

з подоби трикутників отримуємо, що

$$\frac(a)(c)=\frac(H B)(a), \frac(b)(c)=\frac(A H)(b)$$

Звідси маємо, що

$$a^(2)=c \cdot H B, b^(2)=c \cdot A H$$

Склавши отримані рівності, отримуємо

$$a^(2)+b^(2)=c \cdot H B+c \cdot A H$$

$$a^(2)+b^(2)=c \cdot(H B+A H)$$

$$a^(2)+b^(2)=c \cdot A B$$

$$a^(2)+b^(2)=c \cdot c$$

$$a^(2)+b^(2)=c^(2)$$

Що й потрібно було довести.

Геометричне формулювання теореми Піфагора

Теорема

У прямокутному трикутнику площа квадрата, побудованого на гіпотенузі, дорівнює сумі площ квадратів, побудованих на катетах (рис. 2):

Приклади розв'язання задач

приклад

Завдання.Заданий прямокутний трикутник $A B C$, катети якого дорівнюють 6 см і 8 см. Знайти гіпотенузу цього трикутника.

Рішення.Згідно з умовою катети $a=6$ см, $b=8$ см. Тоді, згідно з теоремою Піфагора, квадрат гіпотенузи

$c^(2)=a^(2)+b^(2)=6^(2)+8^(2)=36+64=100$

Звідси отримуємо, що шукана гіпотенуза

$ c = \ sqrt (100) = 10 $ (см)

Відповідь. 10 см

приклад

Завдання.Знайти площу прямокутного трикутника, якщо відомо, що один з його катетів на 5 см більший за інший, а гіпотенуза дорівнює 25 см.

Рішення.Нехай $x$ см - довжина меншого катета, тоді $(x+5)$ см - довжина більшого. Тоді згідно з теоремою Піфагора маємо:

$$x^(2)+(x+5)^(2)=25^(2)$$

Розкриваємо дужки, зводимо подібні та вирішуємо отримане квадратне рівняння:

$x^(2)+5 x-300=0$

Відповідно до теореми Вієта, отримуємо, що

$x_(1)=15$ (см) , $x_(2)=-20$ (см)

Значення $x_(2)$ не задовольняє умові завдання, отже, менший катет дорівнює 15 див, а більший - 20 див.

Площа прямокутного трикутника дорівнює напівтвору довжин його катетів, тобто

$$S=\frac(15 \cdot 20)(2)=15 \cdot 10=150\left(\mathrm(см)^(2)\right)$$

Відповідь.$S=150\left(\mathrm(см)^(2)\right)$

Історична довідка

теорема Піфагора- Одна з основних теорем евклідової геометрії, що встановлює співвідношення між сторонами прямокутного трикутника.

У давньокитайській книзі "Чжоу бі суань цзін" йдеться про піфагоровий трикутник зі сторонами 3, 4 і 5. Найбільший німецький історик математики Моріц Кантор (1829 - 1920) вважає, що рівність $3^(2)+4^(2)=5^ (2) $ було відомо вже єгиптянам ще близько 2300 до н.е. На думку вченого, будівельники будували тоді прямі кути за допомогою прямокутних трикутників зі сторонами 3, 4 та 5. Дещо більше відомо про теорему Піфагора у вавилонян. В одному тексті наводиться наближене обчислення гіпотенузи рівнобедреного прямокутного трикутника.

На даний момент у науковій літературі зафіксовано 367 доказів цієї теореми. Ймовірно, теорема Піфагора є єдиною теоремою з настільки значним числом доказів. Таке різноманіття можна пояснити лише фундаментальним значенням теореми для геометрії.

Потенціал до творчості зазвичай приписують гуманітарним дисциплінам, природно науковим залишаючи аналіз, практичний підхід та суху мову формул та цифр. Математику до гуманітарних предметів не віднесеш. Але без творчості в «цариці всіх наук» далеко не поїдеш – про це людям відомо з давніх-давен. З часів Піфагора, наприклад.

Шкільні підручники, на жаль, зазвичай не пояснюють, що в математиці важливо не лише зубрити теореми, аксіоми та формули. Важливо розуміти та відчувати її фундаментальні принципи. І при цьому спробувати звільнити свій розум від штампів та абеткових істин – лише в таких умовах народжуються всі великі відкриття.

До таких відкриттів можна віднести і те, що сьогодні ми знаємо як теорему Піфагора. З його допомогою ми спробуємо показати, що математика не тільки може, а й має бути цікавою. І що ця пригода підходить не тільки ботанікам у товстих окулярах, а всім, хто міцний розумом і сильним духом.

З історії питання

Строго кажучи, хоч теорема і називається «теорема Піфагора», сам Піфагор її не відкривав. Прямокутний трикутник та його особливі властивості вивчалися задовго до нього. Є дві полярні погляди на це питання. За однією версією Піфагор першим знайшов повноцінний доказ теореми. За іншим доказом не належить авторству Піфагора.

Сьогодні вже не перевіриш, хто має рацію, а хто помиляється. Відомо лише, що докази Піфагора, якщо вона будь-коли існувало, не збереглося. Втім, висловлюються припущення, що знаменитий доказ із «Початків» Евкліда може належати Піфагору, і Евклід його тільки зафіксував.

Також сьогодні відомо, що завдання про прямокутний трикутник зустрічаються в єгипетських джерелах часів фараона Аменемхета I, на вавилонських глиняних табличках періоду правління царя Хаммурапі, в давньоіндійському трактаті «Сульва сутра» та давньокитайському творі «Чжоубі-сунь».

Як бачите, теорема Піфагора займала уми математиків з найдавніших часів. Підтвердженням є і близько 367 різноманітних доказів, які існують сьогодні. У цьому з нею не може тягатися жодна інша теорема. Серед знаменитих авторів доказів можна згадати Леонардо да Вінчі та двадцятого президента США Джеймса Гарфілда. Все це говорить про надзвичайну важливість цієї теореми для математики: з неї виводиться або так чи інакше з нею пов'язана більшість теорем геометрії.

Докази теореми Піфагора

У шкільних підручниках переважно наводять алгебраїчні докази. Але суть теореми в геометрії, тож давайте розглянемо насамперед ті докази знаменитої теореми, які спираються на цю науку.

Доказ 1

Для найпростішого доказу теореми Піфагора для прямокутного трикутника потрібно встановити ідеальні умови: нехай трикутник буде не тільки прямокутним, але й рівнобедреним. Є підстави вважати, що саме такий трикутник спочатку розглядали математику давнини.

Твердження "квадрат, побудований на гіпотенузі прямокутного трикутника, рівновеликий сумі квадратів, побудованих на його катетах"можна проілюструвати наступним кресленням:

Подивіться на рівнобедрений прямокутний трикутник ABC: На гіпотенузі АС можна побудувати квадрат, що складається з чотирьох трикутників, що дорівнює вихідному АВС. А на катетах АВ і ПС побудовано по квадрату, кожен з яких містить по два аналогічні трикутники.

До речі, це креслення лягло основою численних анекдотів і карикатур, присвячених теоремі Піфагора. Найзнаменитіший, мабуть, це «Піфагорові штани на всі боки рівні»:

Доказ 2

Цей метод поєднує в собі алгебру та геометрію і може розглядатися як варіант давньоіндійського доказу математика Бхаскарі.

Побудуйте прямокутний трикутник зі сторонами a, b і c(Рис.1). Потім збудуйте два квадрати зі сторонами, рівними сумі довжин двох катетів, – (a+b). У кожному із квадратів виконайте побудови, як на рисунках 2 та 3.

У першому квадраті збудуйте чотири таких трикутники, як на малюнку 1. У результаті виходить два квадрати: один зі стороною a, другий зі стороною b.

У другому квадраті чотири побудовані аналогічні трикутники утворюють квадрат зі стороною, що дорівнює гіпотенузі. c.

Сума площ збудованих квадратів на рис.2 дорівнює площі збудованого нами квадрата зі стороною з на рис.3. Це легко перевірити, вирахувавши площі квадратів на рис. 2 за формулою. А площа вписаного квадрата на малюнку 3. шляхом віднімання площ чотирьох рівних між собою вписаних у квадрат прямокутних трикутників із площі великого квадрата зі стороною (a+b).

Записавши все це, маємо: a 2 +b 2 =(a+b) 2 – 2ab. Розкрийте дужки, проведіть усі необхідні алгебраїчні обчислення та отримайте, що a 2 +b 2 = a 2 +b 2. У цьому площа вписаного на рис.3. квадрата можна обчислити і за традиційною формулою S=c 2. Тобто. a 2 +b 2 =c 2- Ви довели теорему Піфагора.

Доказ 3

Сам же давньоіндійський доказ описаний у XII столітті в трактаті «Вінець знання» («Сіддханта широмані») і як головний аргумент автор використовує заклик, звернений до математичних талантів та спостережливості учнів та послідовників: «Дивись!».

Але ми розберемо цей доказ більш докладно:

Усередині квадрата побудуйте чотири прямокутні трикутники так, як це позначено на кресленні. Сторону великого квадрата, вона ж гіпотенуза, позначимо з. Катети трикутника назвемо аі b. Відповідно до креслення сторона внутрішнього квадрата це (a-b).

Використовуйте формулу площі квадрата S=c 2, щоб обчислити площу зовнішнього квадрата. І одночасно вирахуйте ту ж величину, склавши площу внутрішнього квадрата і площі всіх чотирьох прямокутних трикутників: (a-b) 2 2+4*1\2*a*b.

Ви можете використовувати обидва варіанти обчислення площі квадрата, щоб переконатися, що вони дадуть однаковий результат. І це дає вам право записати, що c 2 =(a-b) 2 +4*1\2*a*b. В результаті рішення ви отримаєте формулу теореми Піфагора c 2 =a 2 +b 2. Теорему доведено.

Доказ 4

Цей цікавий давньокитайський доказ отримав назву «Стілець нареченої» - через схожу на стілець фігуру, яка виходить в результаті всіх побудов:

У ньому використовується креслення, яке ми вже бачили на рис.3 у другому доказі. А внутрішній квадрат зі стороною з побудований так само, як у давньоіндійському доказі, наведеному вище.

Якщо подумки відрізати від креслення на рис.1 два зелені прямокутні трикутники, перенести їх до протилежних сторін квадрата зі стороною з і гіпотенузами прикласти до гіпотенуз бузкових трикутників, вийде фігура під назвою «стілець нареченої» (рис.2). Для наочності можна те саме зробити з паперовими квадратами і трикутниками. Ви переконаєтеся, що «стілець нареченої» утворюють два квадрати: маленькі зі стороною bі великий зі стороною a.

Ці побудови дозволили давньокитайським математикам і нам слідом за ними дійти висновку, що c 2 =a 2 +b 2.

Доказ 5

Це ще один спосіб знайти рішення для теореми Піфагора, спираючись на геометрію. Називається він "Метод Гарфілда".

Побудуйте прямокутний трикутник АВС. Нам треба довести, що НД 2 =АС 2 +АВ 2.

Для цього продовжіть катет АСта побудуйте відрізок CD, який дорівнює катету АВ. Опустіть перпендикулярний ADвідрізок ED. Відрізки EDі АСрівні. З'єднайте точки Еі У, а також Еі Зі отримайте креслення, як на малюнку нижче:

Щоб довести терему, ми знову вдається до вже випробуваного нами способу: знайдемо площу фігури, що вийшла, двома способами і прирівняємо вирази один до одного.

Знайти площу багатокутника ABEDможна, склавши площу трьох трикутників, які її утворюють. Причому один із них, ЄСВ, не тільки прямокутним, а й рівнобедреним. Не забуваємо також, що АВ = CD, АС = EDі ВС = РЄ– це дозволить нам спростити запис та не перевантажувати його. Отже, S ABED =2*1/2(AB*AC)+1/2ВС 2.

При цьому очевидно, що ABED- Це трапеція. Тому обчислюємо її площу за формулою: S ABED = (DE + AB) * 1/2AD. Для наших обчислень зручніше та наочніше уявити відрізок ADяк суму відрізків АСі CD.

Запишемо обидва способи обчислити площу фігури, поставивши між ними знак рівності: AB*AC+1/2BC 2 =(DE+AB)*1/2(AC+CD). Використовуємо вже відому нам і описану вище рівність відрізків, щоб спростити праву частину запису: AB*AC+1/2BC 2 =1/2(АВ+АС) 2. А тепер розкриємо дужки і перетворюємо рівність: AB*AC+1/2BC 2 =1/2АС 2 +2*1/2(АВ*АС)+1/2АВ 2. Закінчивши всі перетворення, отримаємо саме те, що нам треба: НД 2 =АС 2 +АВ 2. Ми довели теорему.

Звісно, цей список доказів далеко не повний. Теорему Піфагора також можна довести за допомогою векторів, комплексних чисел, диференціальних рівнянь, стереометрії тощо. І навіть фізики: якщо, наприклад, в аналогічних представлених на кресленнях квадратні та трикутні обсяги залити рідину. Переливаючи рідину, можна довести рівність площ і саму теорему у результаті.

Пару слів про Піфагорові трійки

Це питання мало чи взагалі не вивчається у шкільній програмі. А тим часом він дуже цікавий і має велике значення в геометрії. Піфагорові трійки застосовуються на вирішення багатьох математичних завдань. Уявлення про них може стати вам у нагоді в подальшій освіті.

Так що ж таке Піфагорові трійки? Так називають натуральні числа, зібрані по три, сума квадратів двох з яких дорівнює третьому числу в квадраті.

Піфагорові трійки можуть бути:

примітивними (всі три числа – взаємно прості);
не примітивними (якщо кожне число трійки помножити на те саме число, вийде нова трійка, яка не є примітивною).

Ще до нашої ери стародавніх єгиптян заворожувала манія чисел Піфагорових трійок: у завданнях вони розглядали прямокутний трикутник із сторонами 3,4 та 5 одиниць. До речі, будь-який трикутник, сторони якого дорівнюють числам з піфагорової трійки, за замовчуванням є прямокутним.

Приклади Піфагорових трійок: (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20) ), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45), (14 48, 50), (30, 40, 50) і т.д.

Практичне застосування теореми

Теорема Піфагора знаходить застосування у математиці, а й у архітектурі та будівництві, астрономії і навіть літературі.

Спочатку про будівництво: теорема Піфагора знаходить у ньому широке застосування у завданнях різного рівня складності. Наприклад, подивіться на вікно у романському стилі:

Позначимо ширину вікна як bтоді радіус великого півкола можна позначити як Rі виразити через b: R=b/2. Радіус менших півкола також виразимо через b: r=b/4. У цьому завдання нас цікавить радіус внутрішнього кола вікна (назвемо його p).

Теорема Піфагора якраз і стане в нагоді, щоб обчислити р. Для цього використовуємо прямокутний трикутник, що на малюнку позначений пунктиром. Гіпотенуза трикутника складається із двох радіусів: b/4+p. Один катет є радіусом. b/4, інший b/2-p. Використовуючи теорему Піфагора, запишемо: (b/4+p) 2 =(b/4) 2 +(b/2-p) 2. Далі розкриємо дужки та отримаємо b 2 /16+ bp/2+p 2 =b 2 /16+b 2 /4-bp+p 2. Перетворимо цей вираз на bp/2=b 2 /4-bp. А потім розділимо всі члени на b, наведемо подібні, щоб отримати 3/2*p=b/4. І в результаті знайдемо, що p=b/6- Що нам і потрібно.

За допомогою теореми можна обчислити довжину крокви для двосхилого даху. Визначити, якої висоти вежа мобільного зв'язку потрібна, щоб сигнал досягав певного населеного пункту. І навіть стійко встановити новорічну ялинку на міському майдані. Як бачите, ця теорема живе не тільки на сторінках підручників, а й часто буває корисною у реальному житті.

Щодо літератури, то теорема Піфагора надихала письменників з часів античності і продовжує це робити у наш час. Наприклад, німецького письменника ХІХ століття Адельберта фон Шаміссо вона надихнула на написання сонета:

Світло істини розсіється не скоро,
Але, засяявши, розсіється навряд
І, як тисячоліття тому,
Не викликає сумнівів і суперечки.

Наймудріші, коли торкнеться погляду
Світло істини, богів дякують;
І сто биків, заколоті, лежать.
Дар у відповідь Пифагора.

З того часу бики відчайдушно ревуть:
Навіки сполошило бичаче плем'я
Подія, згадана тут.

Їм здається: ось-ось настане час,
І знову їх у жертву принесуть
Якийсь великій теоремі.

(Переклад Віктора Топорова)

А в ХХ столітті радянський письменник Євген Велтистов у книзі «Пригоди Електроніка» доказам теореми Піфагора відвів цілий розділ. І ще півголови розповіді про двомірному світі, який міг би існувати, якби теорема Піфагора стала основним законом і навіть релігією окремо взятого світу. Жити в ньому було б набагато простіше, але й набагато нудніше: наприклад, там ніхто не розуміє значення слів «круглий» та «пухнастий».

А ще у книзі «Пригоди Електроніка» автор вустами вчителя математики Таратара каже: «Головне у математиці – рух думки, нові ідеї». Саме цей творчий політ думки породжує теорема Піфагора - не дарма у неї стільки різноманітних доказів. Вона допомагає вийти за межі звичного і на знайомі речі подивитися по-новому.

Висновок

Ця стаття створена, щоб ви могли заглянути за межі шкільної програми з математики та дізнатися не лише про те докази теореми Піфагора, які наведені в підручниках «Геометрія 7-9» (Л.С. Атанасян, В.М. Руденко) та «Геометрія 7 -11» (А.В. Погорєлов), але й інші цікаві способи довести знамениту теорему. А також побачити приклади, як теорема Піфагора може застосовуватись у звичайному житті.

По-перше, ця інформація дозволить вам претендувати на вищі бали на уроках математики – відомості з предмета з додаткових джерел завжди високо оцінюються.

По-друге, нам хотілося допомогти вам відчути, наскільки математика є цікавою наукою. Переконатися на конкретних прикладах, що завжди є місце творчості. Ми сподіваємося, що теорема Піфагора та ця стаття надихнуть вас на самостійні пошуки та хвилюючі відкриття в математиці та інших науках.

Розкажіть нам у коментарях, чи здалися вам наведені у статті докази цікавими. Чи знадобилися вам ці відомості у навчанні. Напишіть нам, що думаєте про теорему Піфагора та цю статтю – нам буде приємно обговорити все це з вами.

blog.сайт, при повному або частковому копіюванні матеріалу посилання на першоджерело обов'язкове.

теорема Піфагора: Сума площ квадратів, що спираються на катети ( aі b), дорівнює площі квадрата, побудованого на гіпотенузі ( c).

Геометричне формулювання:

Спочатку теорема була сформульована наступним чином:

Алгебраїчне формулювання:

Тобто, позначивши довжину гіпотенузи трикутника через c, а довжини катетів через aі b :

a 2 + b 2 = c 2

Обидві формулювання теореми еквівалентні, але друге формулювання більш елементарне, вона вимагає поняття площі . Тобто друге твердження можна перевірити, нічого не знаючи про площу та вимірявши лише довжини сторін прямокутного трикутника.

Зворотня теорема Піфагора:

Докази

Зрозуміло, концептуально їх можна розбити на малу кількість класів. Найвідоміші з них: докази методом площ, аксіоматичні та екзотичні докази (наприклад, за допомогою диференціальних рівнянь).

Через подібні трикутники

Наступний доказ алгебраїчної формулювання - найпростіший з доказів, що будуються безпосередньо з аксіом. Зокрема, воно не використовує поняття площі фігури.

Нехай ABCє прямокутний трикутник із прямим кутом C. Проведемо висоту з Cі позначимо її основу через H. Трикутник ACHподібний до трикутника ABCпо двох кутах. Аналогічно трикутник CBHподібний ABC. Ввівши позначення

отримуємо

Що еквівалентно

Склавши, отримуємо

Докази методом площ

Нижче наведені докази, незважаючи на їхню простоту, зовсім не такі прості. Всі вони використовують властивості площі, докази яких складніші за доказ самої теореми Піфагора.

Доказ через рівнодоповнюваність

Розташуємо чотири рівні прямокутні трикутники так, як показано на малюнку 1.
Чотирикутник зі сторонами cє квадратом, оскільки сума двох гострих кутів 90 °, а розгорнутий кут - 180 °.
Площа всієї фігури дорівнює, з одного боку, площі квадрата зі стороною (a+b), з другого боку, сумі площ чотирьох трикутників і двох внутрішніх квадратів.

Що й потрібно було довести.

Докази через рівноскладність

Елегантний доказ за допомогою перестановки

Приклад одного з таких доказів вказано на кресленні праворуч, де квадрат, побудований на гіпотенузі, перестановкою перетворюється на два квадрати, побудованих на катетах.

Доказ Евкліда

Креслення до доказу Евкліда

Ілюстрація до доказу Евкліда

Ідея доказу Евкліда полягає в наступному: спробуємо довести, що половина площі квадрата, побудованого на гіпотенузі, дорівнює сумі половин площ квадратів, побудованих на катетах, а тоді площі великого і двох малих квадратів рівні.

Розглянемо креслення зліва. На ньому ми побудували квадрати на сторонах прямокутного трикутника і провели з вершини прямого кута С промінь перпендикулярно до гіпотенузи AB, він розсікає квадрат ABIK, побудований на гіпотенузі, на два прямокутники - BHJI і HAKJ відповідно. Виявляється, що площі даних прямокутників точно рівні площам квадратів, побудованих на відповідних катетах.

Спробуємо довести, що площа квадрата DECA дорівнює площі прямокутника AHJK Для цього скористаємося допоміжним спостереженням: Площа трикутника з тією самою висотою та основою, що й даний прямокутник дорівнює половині площі заданого прямокутника. Це наслідок визначення площі трикутника як половини добутку основи висоту. З цього спостереження випливає, що площа трикутника ACK дорівнює площі трикутника AHK (не зображеного на малюнку), яка, у свою чергу, дорівнює половині площі прямокутника AHJK.

Доведемо тепер, що площа трикутника ACK також дорівнює половині площі квадрата DECA. Єдине, що необхідно для цього зробити, - це довести рівність трикутників ACK і BDA (оскільки площа трикутника BDA дорівнює половині площі квадрата за вказаною вище властивістю). Рівність це очевидно, трикутники рівні з обох боків та кутку між ними. Саме - AB=AK,AD=AC - рівність кутів CAK і BAD легко довести методом руху: повернемо трикутник CAK на 90° проти годинникової стрілки, тоді очевидно, що відповідні сторони двох трикутників, що розглядаються, збігатимуться (через кут при вершині квадрата - 90 °).

Міркування про рівність площ квадрата BCFG і прямокутника BHJI абсолютно аналогічне.

Тим самим було доведено, що площа квадрата, побудованого на гіпотенузі, складається з площ квадратів, побудованих на катетах. Ідея цього доказу додатково проілюстрована за допомогою анімації, яка розташована вище.

Доказ Леонардо да Вінчі

Головні елементи доказу – симетрія та рух.

Розглянемо креслення, як видно з симетрії, відрізок CIрозсікає квадрат ABHJ на дві однакові частини (оскільки трикутники ABCі JHIрівні за побудовою). Користуючись поворотом на 90 градусів проти годинникової стрілки, ми вбачаємо рівність заштрихованих фігур CAJI і GDAB . Тепер ясно, що площа заштрихованої нами фігури дорівнює сумі половин площ квадратів, побудованих на катетах, та площі вихідного трикутника. З іншого боку, вона дорівнює половині площі квадрата, побудованого на гіпотенузі плюс площа вихідного трикутника. Останній крок у доказі надається читачеві.

Доказ методом нескінченно малих

Наступний доказ за допомогою диференціальних рівнянь часто приписують відомому англійському математику Харді, який жив у першій половині XX ст.

Розглядаючи креслення, показане на малюнку, і спостерігаючи зміну сторони a, ми можемо записати наступне співвідношення для нескінченно малих прирощень сторін зі a(використовуючи подобу трикутників):

Доказ методом нескінченно малих

Користуючись методом поділу змінних, знаходимо

Більше загальний вираз зміни гіпотенузи у разі прирощень обох катетов

Інтегруючи дане рівняння та використовуючи початкові умови, отримуємо

c 2 = a 2 + b 2+ constant.

Таким чином, ми приходимо до бажаної відповіді

c 2 = a 2 + b 2 .

Як неважко бачити, квадратична залежність у остаточній формулі з'являється завдяки лінійній пропорційності між сторонами трикутника та прирощеннями, тоді як сума пов'язана з незалежними вкладами від прирощення різних катетів.

Простіший доказ можна отримати, якщо вважати, що один із катетів не відчуває прирощення (в даному випадку катет b). Тоді для константи інтегрування отримаємо

Варіації та узагальнення

Якщо замість квадратів побудувати на катетах інші подібні фігури, то вірно наступне узагальнення теореми Піфагора: У прямокутному трикутнику сума площ подібних фігур, побудованих на катетах, дорівнює площі фігури, побудованої на гіпотенузі.Зокрема:
- Сума площ правильних трикутників, побудованих на катетах, дорівнює площі правильного трикутника, побудованого на гіпотенузі.
- Сума площ півколів, побудованих на катетах (як діаметрі), дорівнює площі півкола, побудованого на гіпотенузі. Цей приклад використовується при доказі властивостей фігур, обмежених дугами двох кіл і носять ім'я гіпократових луночек.

Історія

Чу-пей 500-200 до н. Зліва напис: сума квадратів довжин висоти та основи є квадрат довжини гіпотенузи.

У давньокитайській книзі Чу-пей йдеться про піфагоровий трикутник зі сторонами 3, 4 і 5: У цій же книзі запропоновано малюнок, який збігається з одним із креслень індуської геометрії Басхари.

Кантор (найбільший німецький історик математики) вважає, що рівність 3 + 4 + 5 = було відомо вже єгиптянам ще близько 2300 до н. е.., за часів царя Аменемхета I (згідно з папірусом 6619 Берлінського музею). На думку Кантора гарпедонапти, або натягувачі мотузок, будували прямі кути за допомогою прямокутних трикутників зі сторонами 3, 4 і 5.

Дуже легко можна відтворити їхній спосіб побудови. Візьмемо мотузку завдовжки 12 м і прив'яжемо до неї по кольоровій смужці на відстані 3м. від одного кінця та 4 метри від іншого. Прямий кут виявиться ув'язненим між сторонами завдовжки 3 і 4 метри. Гарпедонаптам можна було б заперечити, що їх спосіб побудови ставати зайвим, якщо скористатися, наприклад, дерев'яним косинцем, що застосовується всіма теслярами. Відомі єгипетські малюнки, на яких зустрічається такий інструмент, наприклад малюнки, що зображують столярну майстерню.

Дещо більше відомо про теорему Піфагора у вавилонян. В одному тексті, що відноситься до часу Хаммурабі, тобто до 2000 до н. е., наводиться наближене обчислення гіпотенузи прямокутного трикутника. Звідси можна дійти невтішного висновку, що у Дворіччя вміли робити обчислення з прямокутними трикутниками, по крайнього заходу у деяких випадках. Грунтуючись, з одного боку, на сьогоднішньому рівні знань про єгипетську та вавілонську математику, а з іншого – на критичному вивченні грецьких джерел, Ван-дер-Варден (голландський математик) зробив такий висновок:

Література

Російською мовою

Скопець З. А.Геометричні мініатюри. М., 1990
Єленьський Щ.Слідами Піфагора. М., 1961
Ван-дер-Варден Б. Л.Пробуджена наука. Математика Стародавнього Єгипту, Вавилону та Греції. М., 1959
Глейзер Г. І.Історія математики у школі. М., 1982
Ст Літцман, «Теорема Піфагора» М., 1960.
- Сайт про теорему Піфагора з великою кількістю доказів матеріал узятий із книги В.Літцмана, велика кількість креслень представлена у вигляді окремих графічних файлів.
Теорема Піфагора і трійки Піфагора глава з книги Д. В. Аносова «Погляд на математику і щось з неї»
Про теорему Піфагора та способи її доказу Г. Глейзер, академік РАВ, Москва

Англійською

Теорема Піфагора на WolframMathWorld (англ.)
Cut-The-Knot, секція присвячена теоремі піфагора, близько 70 доказів та додаткова інформація (англ.)

Wikimedia Foundation. 2010 .